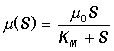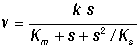Ферменты представляют собой высокоспециализированные белковые катализаторы,
ускоряющие течение биохимических реакций в сотни тысяч, миллионы раз. Любое
ферментативное превращение начинается со связывания молекул субстратов с
активным центром фермента и завершается разрывом этих связей. Гипотеза об образовании лабильного субстрат-ферментного комплекса
была впервые высказана в 1902 г. Брауном и Анри. Пытаясь дать
количественное толкование явлению насыщения амилазных реакций субстратами Анри в
1904 г. допустил, что реакция образования фермент-субстратного комплекса
находится в равновесии и вывел уравнение начальной скорости реакции
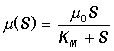
К этому же уравнению пришли в 1914 г. Михаэлис и
Метен, а позднее в 1925 г. Бриггс и Холдейн,
которые получили аналогичное выражение в предположении квазистационарности
реакции образования фермент-субстратного комплекса. В 1943 г. Чанс
экспериментально подтвердил образование такого комплекса спектрофотометрическим
методом и проследил за изменением его концентрации в ходе реакции,
катализируемой гемосодержащим ферментом пероксидазой. В 1930 г. Холдейн
распространил теоретические представления о фермент-субстратном комплексе на
случай двусубстратных и обратимых реакций и постулировал существование различных
фермент-субстратных, фермент-продуктных и фермент-ингибиторных промежуточных
комплексов. В настоящее время множество таких комплексов экспериментально
изучено.
Учет наличия ингибиторов в системе, в частности в случае, когда в качестве
ингибитора выступают молекулы субстрата, образующие как активные, так и
неактивные комплексы с субстратом, приводит к более сложным нелинейным
выражениям для скорости реакции:
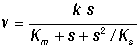
Наличие такого типа нелинейности обусловливает важные свойства ферментативных систем:
Анализ кинетических
особенностей различных схем ферментативных реакций с помощью представлений на
фазовой плоскости и в параметрическом пространстве, детально представлен в [.
Дополнительная информация:
© 2001-2023 Кафедра биофизики МГУ