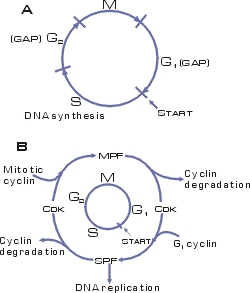
Рис. 11. Схема клеточного
цикла. В процессе жизненного цикла клетка удваивает свое содержимое и делится на
две. В организме млекопитающего для поддержания жизни производятся ежесекундно
миллионы новых клеток. Нарушение регуляции пролиферации клеток проявляется как
онкологическое заболевание. Этим вызван большой интерес к изучению и
моделированию механизмов регуляции клеточного деления. {{[75104, 75110]}}.
Клеточный цикл состоит из двух периодов:
Митоз (М-фаза) включает
разделение предварительно удвоенного ядерного материала, деление ядра и
деление самой клетки - цитокинез и занимает около часа.
интерфаза, включающая стадию роста
G1, фазу репликации
ДНК (S), фазу подготовки к
делению G2.
Клеточный цикл регулируется генами и белками-ферментами двух основных
классов. Циклин-зависимые протеин-киназы (Cdk) индуцируют
последовательность процессов путем фосфорилирования отдельных белков. Циклины,
которые синтезируются и деградируют при каждом новом цикле деления, связываются
с молекулами Cdk и контролируют их способность к
фосфорилированию, без циклина Cdk не активны. Количество
этих молекул-регуляторов различно в разного вида клетках. В делении дрожжевой
клетки основные роли играют один Cdk и девять циклинов,
которые образуют девять разных циклин-Cdk комплексов. У
гораздо более сложно организованных млекопитающих изучено шесть Cdk и полтора десятка циклинов. Контроль выхода клетки из G1, и G2 фаз
осуществляют промотор-фактор S-фазы (SPF) и промотор-фактор M-фазы (MPF), представляющие собой гетеродимеры. Cуществует особая
контрольная точка клеточного цикла (Start), с которой
заканчивается рост (G1 фаза) и начинается
процесс синтеза ДНК.
 |
Рис. 11. Схема клеточного
цикла. |
Простая модель процесса предложена Тайсоном (Tyson,
1995). Постулируется существование фактора транскрипции
SBF, который может быть в активной Sa и
пассивной Si форме. Он переходит в активную
форму под действием циклина Cln (N) и Start-киназы (Cdc28-Cln3) (A) и инактивируется другим
веществом (E). Циклин продуцируется путем активации SBF и деградирует. SBF активируется
Chu и Start-киназой и
инактивируется фосфатазой. Безразмерная модель процессов имеет вид:
Модель имеет одно или три стационарных решения (два устойчивых) в засимости
от значений параметров, и при увеличении параметра a (в процессе роста клетки) описывает
переключение системы из G1 в S фазу.
Добавление двух уравнений сходного вида позволяет описать также переключение
из G2 в фазу митоза M.
Полная модель, учитывающая и другие регуляторные ферменты в фосфорилированной и
дефосфорилированной форме содержит 9 нелинейных уравнений (Novak, Tyson 1993) и хорошо описывает кинетику деления
ооцитов Xenopus. При соответствующем подборе параметров она применима к описанию
деления других типов клеток. Большое количество работ было посвящено попыткам
моделирования периодического воздействия на клеточный цикл с целью оптимизации
параметров рентгено- радио- или хемотерапии при воздействии на клетки
онкологических опухолей.
В современной литературе по математической биологии рассмотрены тысячи автоколебательных систем на разных уровнях организации живой природы. Несомненно, колебательный характер процессов - эволюционное изобретение природы, и их функциональная роль имеет несколько разных аспектов. Во-первых колебания позволяют разделить процессы во времени, когда в одном компартменте клетки протекает сразу несколько различных реакций, организуя периоды высокой и низкой активности отдельных метаболитов. Во-вторых, характеристики колебаний, их амплитуда и фаза, несут определенную информацию и могут играть регуляторную роль в каскадах процессов, проходящих на уровне клетки и живого организма. Наконец, колебательные (потенциально или реально) системы служат локальными элементами распределенных активных сред, способных к пространственно-временной самоорганизации, в том числе к процессам морфогенеза.
Внутриклеточные колебания задают эндогенные биологические ритмы
(биологические часы), которые свойственны всем живым системам [.
Именно они определяют периодичность деления клеток, отмеряют время рождения и
смерти живых организмов. Модели колебательных систем типа (27-30)
используются в ферментативном катализе, теории иммунитета, в теории
трансмембранного ионного переноса, микробиологии и биотехнологии.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ