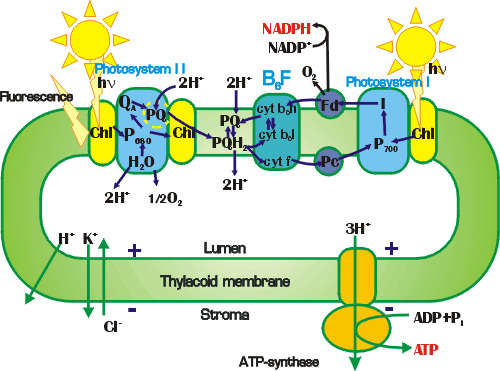
Рис. 19. Схема процессов в
хлоропласте. Система первичных процессов фотосинтеза в настоящее время является одной из наиболее хорошо экспериментально изученных биологических систем. Этим определяется возможность построения успешных математических моделей системы в целом и ее фрагментов. Биохимическими, генетическими методами, методами рентгеноструктурного анализа определен состав и молекулярная структура компонентов фотосинтетического аппарата.
Система первичных процессов обладает еще одним чрезвычайно важным свойством, отличающим ее от других биологических систем. Система "включается" светом, и ее можно тестировать как радиотехническое устройство, с помощью дельта-образных (лазерная вспышка) или прямоугольных (включение постоянного света) импульсов. Поэтому при ее исследовании чрезвычайно эффективными оказываются спектральные методы (дифференциальная и импульсная спектрофотометрия в полосах поглощения отдельных молекул - участников первичных реакций, флуорометрия, методы электронного парамагнитного и ядерного магнитного резонанса и др.). Важным является и то обстоятельство, что из фотосинтезирующей органеллы - тилакоида можно выделить биохимическими методами отдельно фрагменты фотосинтетических реакционных центров фотосистем 1 и 2 (из хромотофоров фотосинтезирующих бактерий - бактериальные реакционные центры), при этом выделенные фрагменты фотосистем сохраняют способность к поглощению света и светоиндуцированному разделению зарядов. Химически модифицируя состав таких фрагментов, изменяя характер освещения, окислительно-восстановительные условия, pH среды, можно спектральными методами наблюдать релаксационные процессы и делать вывод о кинетических характеристиках системы, в первую очередь о константах скоростей переноса электрона на отдельных участках фотосинтетической электрон-транспортной цепи. Именно благодаря этим особенностям система первичных процессов фотосинтеза оказалась благодатным объектом для математического моделирования.
Важной задачей математического моделирования является идентификация
параметров системы - оценка констант скоростей отдельных реакций по
экспериментальным кривым, отражающим изменение во времени концентрации того или
иного компонента. При этом часто экспериментально можно зарегистрировать
изменение только одного или нескольких компонентов (например, сигнал ЭПР
фотоактивного пигмента фотосистемы 1) и по математической модели
идентифицировать константы скоростей процессов переноса электрона в
фотореакционном центре на других участках цепи. Из математической теории
идентификации известно, что однозначно такую оценку можно сделать лишь для
линейных систем с полностью наблюдаемым вектором состояний. Естественно, что для
реальных систем это условие не выполняется. Однако, используя дополнительные
экспериментальные данные, такую оценку можно сделать для относительно простых
систем, например, для выделенных фотореакционных центров [.
В целостной, нефрагментированной системе, хлоропласте зеленых растений или
хроматофоре бактерий, включающей всю совокупность компонентов фотосинтетического
аппарата, регистрируемые кинетические кривые, как правило, носят сложный
характер, поскольку они отражают взаимосвязь многих процессов. Извлечь из таких
кривых информацию о кинетических параметрах системы можно только с помощью
математической модели. При этом возникает проблема сопряжения знаний и
представлений об отдельных стадиях фотосинтетических процессов, изученных
порознь и методами разных наук, в единую схему.
Определяющими в каскаде фотосинтетических процессов являются первичные процессы:
[Рубин А. Б. Биофизика; Ризниченко Г. Ю. Математические модели первичных процессов фотосинтеза].
В результате первичных процессов фотосинтеза образуются макроэргические
соединения АТФ из АДФ и неорганического фосфата, а также восстановленные
пиридонуклеотиды, необходимые для работы цикла Кальвина
восстановления СО2 и образования глюкозы. Все
эти процессы происходят в мембране тилакода в структурах, схематически
изображенных на рис.
19.
 |
Рис. 19. Схема процессов в
хлоропласте. |
В первых моделях фотосинтетического электронного транспорта (60-70 годы)
реакцию переноса с молекулы-донора на молекулу-акцептор описывали с помощью
закона действующих масс, считая, что скорость реакции пропорциональна
произведению концентраций реагентов (бимолекулярные реакции). Однако, как видно
из рис.
19, транспортные процессы здесь происходят не путем случайных
столкновений, а в фиксированных комплексах переносчиков. В настоящее время
расшифрованы не только химический состав, но и координаты отдельных атомов
молекул, участвующих в переносе электрона, можно указать "электронную тропу", то
есть путь электрона с одного атома на другой в пределах одной молекулы.
Степень детализации описания процессов определяется целями моделирования.
Обычно рассматривают каждую молекулу как переносчик, который может находиться в
одном из состояний - нейтральном (окисленном) - без
электрона, и восстановленном (нейтральном) - с
электроном. Возможно также рассмотрение различных конформационных состояний,
протонированного и депротонированного состояний и проч.
В общем виде, если комплекс состоит из n переносчиков, состояния комплекса
®
[C1C2...Cn] ®Ci,
составляющих комплекс.
Переходы между состояниями описываются уравнениями, линейными относительно
вероятностей состояний: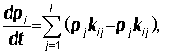 с
начальными условиями
с
начальными условиями pi(0) = b, i = 1, ..., l.
Или, в векторном виде:
dP / dt = Kr P, P(0) = B,
Вероятность найти переносчик в интересующем нас состоянии L представляет собой сумму вероятностей тех состояний
комплекса, в которых переносчик представлен в данном состоянии.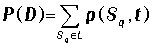
Чем точнее представления о процессах, протекающих в комплексе, тем более
детальная схема может быть составлена, и тем большее число уравнений требуется
для описания переходов между состояниями. Так, переходы между состояниями
комплекса фотосистемы 2, определяющие процессы флуоресценции, представлены на
рис.
20. Благодаря сильному различию величин констант скоростей на
отдельных участках цепи (быстрые переходы обозначены пунктирными стрелками), с
учетом временной иерархии система может быть редуцирована, и дифференциальные
уравнения для быстрых переменных заменены алгебраическими.
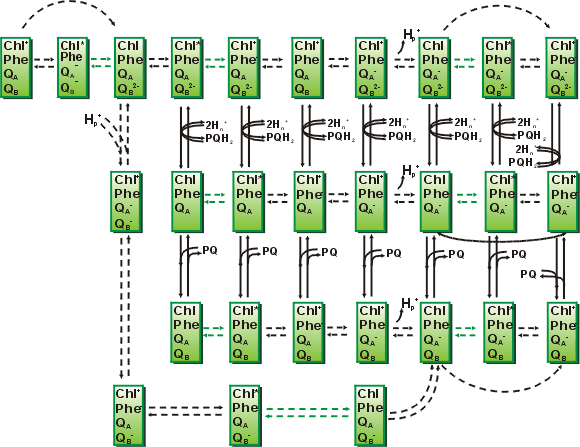 |
Рис. 20. Схема переходов между
состояниями в фотосистеме 2 высших растений. |
Цитохромный комплекс и комплекс фотосистемы 1 также характеризуются набором большого числа состояний. Модель, описывающая, кроме того, взаимодействие между комплексами, ионные потоки, работу АТФ-синтетазы, содержит десятки уравнений и сотни параметров, многие из которых известны из литературы. Однако эти параметры оценены для разных объектов и при разных условиях, чаще всего их оценивают в экспериментах на выделенных фрагментах, элементарные константы скоростей реакций для которых могут быть иными, чем для целых хлоропластов. Поэтому при включении в модель величины параметров, как правило, требуют уточнения.
Сопоставление результатов детального математического моделирования и
идентификации параметров математических моделей для отдельных фотосинтезирующих
комплексов, этих же комплексов в сложной системе взаимодействующих компонентов и
редуцированных моделей взаимодействия фотосинтетических процессов позволяет
заключить, что регуляторные свойства системы различны на разных уровнях иерархии
сложности происходящих в них процессов. На уровне фотосинтетических реакционных
центров управление жесткое. Квант света вызывает строгую последовательность
процессов, его поглощение приводит к перераспределению зарядов и конформационным
изменениям, направленным на быстрейший вынос электрона за пределы
фотосинтетической пары. Сами фотосинтетические реакционные центры в большой
степени "стандартизированы" - их организация аналогична для ФС1, ФС2 и бактериальных центров.
Идентификация математических моделей, по экспериментальным данным подтверждает,
что параметры мало меняются при изменении внешних условий, таких как рН, редокс
потенциал, вязкость среды и др. Кинетические паттерны процессов, происходящих в
этих центрах имеют, как правило, характер простой релаксации.
На уровне взаимодействия фотосистем регуляция имеет более "гибкий" характер. Диффузионные стадии здесь существенно зависят от рН, редокс условий, вязкости, что делает возможным регуляцию этих стадий со стороны клеточного и организменного уровня при изменении внешних факторов и в процессе роста. Кинетические паттерны более сложные, они могут содержать несколько максимумов, что проявляется в характерных формах кривых индукции флуоресценции в минутном временном диапазоне.
С накоплением знаний о структуре и строении фотосинтетического аппарата, деталях его организации и ростом возможностей вычислительной техники, математическое моделирование первичным процессов фотосинтеза все более становится действенным инструментом перевода данных спектральных измерений на язык кинетических параметров и далее, с помощью компьютерной визуализации, на язык структурных изменений фотосинтетического аппарата.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ