Дискретные модели популяций с неперекрывающимися поколениями
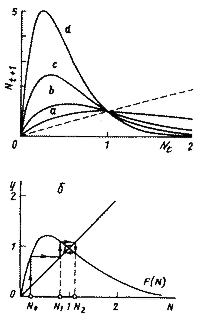
Рис.5. Модели популяций с неперекрывающимися поколениями. а. Вид одноэкстремальной функции зависимости численности популяции в данный момент времени от численности в предыдущий момент времени. Nt+1=F(Nt); б. Определение значений численности популяции в последовательные моменты времени (см. текст) для дискретного аналога логистического уравнения (12). |
Даже в таких популяциях, где особи размножаются несколько лет подряд (млекопитающие и птицы, многолетние растения), наличие сезонов размножения вносит некоторое запаздывание в процессы регуляции численности. Если же взрослые особи, размножающиеся в данном году, редко или никогда не доживают до того, чтобы размножиться в будущем году, как, например, у однолетних растений, мелких грызунов, многих насекомых, это оказывает существенное влияние на динамику их численности. В этом случае уравнение (7) следует заменить уравнением
Nn+1=N(xn), (11)
где Nn - численность популяции в году n.
Наблюдения над динамикой численности показывают, что в таких системах при малых численностях N растет от одной генерации к другой, а при высоких - падает. Это свойство - резко расти при малых N и падать при больших, проявляется в экономике как закон "бумов и спадов". В таких случаях функция F - одноэкстремальная, вид ее изображен на рис. 5а.
Функция такого типа может быть описана с помощью различных формул. Ниболее широко распространена версия дискретного логистического уравнения, предложенная Мораном для численности насекомых (1950) и Рикером для рыбных популяций (1954):
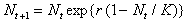 (12)
(12)
Здесь, как и в логистическом уравнении (3), r-константа собственной скорости роста, K - емкость экологической ниши популяции. Ход решения уравнения (12) можно наглядно продемонстрировать графически с помощью диаграммы и лестницы Ламерея. Точка пересечения биссектрисы первого координатного угла Nt+1=Nt и функции F(Nt) определяет равновесное состояние системы, аналогичное стационарному состоянию дифференциального уравнения. На рис. 5б показан способ нахождения значений Nt в последовательные моменты времени. Пусть в начальный момент времени N=N0. F(N0)=N1 задает значение численности в последующий момент времени t=1. Величина N1 в свою очередь определяет значение F(N1)=N2. И так далее. На рис. 5б изображен случай, когда траектория сходится к равновесному состоянию, совершая затухающие колебания.

Рис.6. Типы динамики численности в модели популяции с неперекрывающимися поколениями при разных значениях собственной скорости роста. а.- Монотонный рост; б.- Затухающие колебания; в.- двухточечный цикл; г.- четырехточечный цикл; д, е- квазистохастическое поведение. |
В зависимости от крутизны графика функции F(N1) (кривые a,b,c,d на рис. 6) в системе могут возникать самые разнообразные режимы. С ростом r поведение усложняется. Монотонное стремление к равновесию (Рис.6а) сменяется колебательным (Рис.6б). При дальнейшем увеличении r (увеличении крутизны кривой F(N1)) возникают циклы - аналоги предельных циклов для систем дифференциальных уравнений (рис. 6 в,г). Если r еще больше растет - наблюдается квазистохастическое поведение - хаос. (рис. 6 д,е). Модели такого типа являются простейшими детерминированными объектами, демонстрирующими квазистохастическое поведение.
Квазистохастическим поведением могут обладать и переменные в непрерывных нелинейных автономных системах трех и более дифференциальных уравнений. Изображение детерминированного хаоса в популяции из трех видов: хишник - две жертвы представлено на рис.12. Таким образом, стохастичность может быть свойством, присущим самим детерминированным природным системам (Детерминированный хаос), и не зависит от того, какой математический аппарат, непрерывный или дискретны, используется.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ

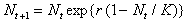 (12)
(12)