Структурные модели популяций
Основные механизмы, управляющие поведением популяции, могут быть связаны с дифференциацией особей. Таким определяющим фактором является половая структура популяции. Общеизвестна также роль возрастной структуры - так называемые возрастные пирамиды. Например, при моделировании динамики древостоев наибольший интерес представляет не столько численность, сколько запас стволовой древесины, средние высота и диаметр деревьев (и их дисперсия).
Обобщение моделей на случай, когда особь в популяции характеризуется не только возрастом, весом или размером,, но одновременно многими факторами, привело к формированию структурных моделей популяций (individual based models) которая является одной из наиболее интенсивно развивающихся за последние 20 лет ветвей математической биологии. (Metz J.A.J., Denkman O. (eds)/ The Dynamics of Physiologically structured populations. Lecture Notes in Biomath., 68, Springer,1986). Теоретическая цель таких моделей - описать поведение популяции в терминах поведения индивидов. Понятно, что расчет структурных моделей требует достаточно продвинутой вычислительной техники.
Структурная модель популяций имеет два уровня описания - индивидуальный и популяционный. На индивидуальном уровне выбирается набор фазовых (структурных) переменных 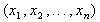 . В каждый момент времени индивидум характеризуется возрастом а и состоянием X=
. В каждый момент времени индивидум характеризуется возрастом а и состоянием X=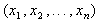 . Затем задается пространство состояний индивидуума - область в n-мерном пространстве, динамика состояний индивидуума (обычно, система обыкновенных дифференциальных уравнений), интенсивность гибели индивидуумов, интенсивность рождения от отдельной особи и распределение новорожденных по пространству состояний, влияние внешней среды и состояния популяции в целом на скорость роста индивидуума и интенсивности рождения и гибели.
. Затем задается пространство состояний индивидуума - область в n-мерном пространстве, динамика состояний индивидуума (обычно, система обыкновенных дифференциальных уравнений), интенсивность гибели индивидуумов, интенсивность рождения от отдельной особи и распределение новорожденных по пространству состояний, влияние внешней среды и состояния популяции в целом на скорость роста индивидуума и интенсивности рождения и гибели.
Популяционный уровень задается начальным распределением индивидуумов, уравнением на текущее распределение популяции (это уравнение неразрывности или уравнение Колмогорова), общим количеством новорожденнных в единицу времени, вычисляемым по интенсивности рождения и текущему распределению популяции.
Таким образом, структурная модель состоит из трех блоков:
- динамическая система, описывающая развитие отдельной особи в популяции
- уравнение неразрывности на плотность популяции в пространстве состояний
- интегральное граничное условие на плотность популяции, описывающее процесс возобновления.
Первые структурные модели появились в области микробиологии, где они оказались чрезвычайно плодотворными для использования в биотехнологии с целью оптимизации процесса получения определенных веществ, входящих в состав микроорганизмов, или метаболитов - продуктов жизнедеятельности культивируемых микроорганизмов. (Ramkrishna D et.al., 1967; Frederickson A..G., 1976). Наряду с возрастом и размерами микроорганизмов в качестве переменных, характеризующих отдельный микроорганизм в эти модели входило содержание в нем нуклеиновых кислот и других жизненно важных элементов, определяющих скорость роста биомассы и характерное время деления клеток микроорганизмов, а также содержание вещества, являющегося целевым продуктом биотехнологического процесса. В последние годы структурная теория популяций получила широкое применение при моделировании лесных сообществ.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ
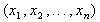 . В каждый момент времени индивидум характеризуется возрастом а и состоянием X=
. В каждый момент времени индивидум характеризуется возрастом а и состоянием X=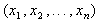 . Затем задается пространство состояний индивидуума - область в n-мерном пространстве, динамика состояний индивидуума (обычно, система обыкновенных дифференциальных уравнений), интенсивность гибели индивидуумов, интенсивность рождения от отдельной особи и распределение новорожденных по пространству состояний, влияние внешней среды и состояния популяции в целом на скорость роста индивидуума и интенсивности рождения и гибели.
. Затем задается пространство состояний индивидуума - область в n-мерном пространстве, динамика состояний индивидуума (обычно, система обыкновенных дифференциальных уравнений), интенсивность гибели индивидуумов, интенсивность рождения от отдельной особи и распределение новорожденных по пространству состояний, влияние внешней среды и состояния популяции в целом на скорость роста индивидуума и интенсивности рождения и гибели.