Рассмотрим теперь некоторые модели, в которых моделируется совместная трансформация нескольких биогенных элементов. Чаще всего такими элементами являются азот и фосфор. В некоторых моделях, помимо азота и фосфора, рассматривается также трансформация углерода и/или кремния.
В работах (Йоргенсен, 1985; Jorgensen, 1976) построена модель эвтрофикации, которая рассматривает трансформацию углерода, азота и фосфора. Она реализована и подтверждена применительно к пяти конкретным объектам. Модель включает в себя 17 переменных состояния. Число слоев в разбираемом варианте модели равно единице, поэтому он пригоден только для описания мелководных озер и прудов. В модели рассматриваются три трофических уровня: фитопланктон, зоопланктон и рыбы. Последние, однако, не рассматриваются в качестве переменной состояния, а их численность принимается примерно постоянной. Развитие фитопланктона описывается как процесс, складывающийся из двух стадий: поглощения биогенных веществ в соответствии с кинетикой Моно и роста, определяемого концентрациями внутриклеточных субстратов. Другими словами, рассматриваются независимые круговороты биогенных элементов - фосфора, азота и углерода. Это означает, что биомасса фитопланктона, а также содержащиеся в клетках водорослей углерод, фосфор и азот должны быть включены в качестве переменных состояния. Такой подход по сравнению с подходом, предполагающим постоянство стехиометрических соотношений, довольно сложен, однако, как показал Йоргенсен (Jorgensen, 1976), при использовании для описания развития водорослей упрощенной постулированной кинетики Моно добиться точного воспроизведения времени достижения максимальной концентрации и продуктивности фитопланктона невозможно. Для соблюдения принципа сохранения массы в модель введены переменные, отражающие содержание азота и фосфора как в зоопланктоне, так и в рыбах.
Процесс минерализации детрита описан в модели реакцией первого порядка с различными постоянными скорости для азота и фосфора. Растворенные неорганические азот и фосфор включены в модель в качестве переменных состояния, а растворенный неорганический углерод (главным образом, в виде ![]() ) - не включен, поскольку концентрация бикарбонат-ионов, как правило, велика и далека от лимитирующей.
) - не включен, поскольку концентрация бикарбонат-ионов, как правило, велика и далека от лимитирующей.
В модели используются следующие агрегированные переменные:
СС - концентрация углерода в клетках водорослей (![]() );
);
FNF - относительное содержание азота в рыбах;
FNZ - относительное содержание азота в зоопланктоне;
FPF - относительное содержание фосфора в рыбах;
FPZ - относительное содержание фосфора в зоопланктоне;
NC - концентрация азота в клетках водорослей (![]() );
);
ND - содержание детритного азота (![]() );
);
NSED - содержание азота в донных отложениях в пересчете на единицу объема воды водоема (![]() );
);
NS - содержание растворенного азота (![]() );
);
PB - содержание биологически мобилизуемого фосфора в донных отложениях в пересчете на единицу объема воды водоема (![]() );
);
PC - концентрация фосфора в клетках водорослей (![]() );
);
PD - концентрация детритного фосфора (![]() );
);
PE - содержание обменного фосфора в пересчете на единицу объема воды водоема (![]() );
);
PHYT - биомасса фитопланктона (![]() );
);
PI - содержание фосфора в интерстициальной воде в пересчете на единицу объема воды водоема (![]() );
);
PS - концентрация растворимого фосфора (![]() );
);
ZOO - биомасса зоопланктона (![]() ).
).
Параметры модели с указанием их экологического смысла и их численные значения, которые были использованы при проведении расчетов, представлены в таблице 1.
Таблица 1. Отдельные параметры модели.
| Обозначение | Определение | Величина | Единица измерения |
| Коэффициент поглощения света водой | 0,27 | ||
| Концентрационный коэффициент поглощения света фитопланктоном | 0,18 | ||
| С | Концентрация неорганического углерода | 100,0 | |
| Максимальная скорость роста фитопланктона | 2,53 | ||
| D | Глубина | m | |
| DB | Глубина биологически высокоактивного слоя | 2?10-3 | m |
| DENIT | Константа денитрификации | 0,03 | |
| DMU | Относительное содержание сухого вещества в осадках | 0,07 | - |
| Концентрация ихтиомассы | |||
| KA | Константа Михаэлиса для выедания фитопланктона зоопланктоном | 2,0 | |
| KC | Константа Михаэлиса для поглощения углерода | 0,5 | |
| Константа минерализации детритного азота при 10°С | 0,1 | ||
| Константа минерализации детритного фосфора при 10°С | 0,4 | ||
| Константа минерализации обменного фосфора донных отложений при 20°С | 2,2?10-4 | ||
| KL | Константа Михаэлиса для солнечной радиации | 400,0 | |
| KN | Константа Михаэлиса для поглощения азота | 0,2 | |
| KP | Константа Михаэлиса для поглощения фосфора | 0,02 | |
| KREL | Константа скорости процесса перехода азота из донных отложений в толщу воды | 0,004 | |
| KS | Пороговая концентрация зоопланктона | 0,75 | |
| KZ | Константа Михаэлиса для выедания зоопланктона рыбами | 0,35 | |
| LUL | Толщина активного слоя донных отложений | 0,1 | m |
| DS | m | ||
| MA | Мгновенный коэффициент смертности фитопланктона | ||
| Максимальная скорость роста зоопланктона | 0,188 | ||
| MZ | Мгновенный коэффициент смертности зоопланктона | 0,033 | |
| Максимальная удельная скорость выедания зоопланктона рыбами | 0,012 | ||
| Максимальная интенсивность дыхания фитопланктона | 0,088 | ||
| Максимальная интенсивность дыхания зоопланктона | 0,028 | ||
| SVD | Скорость оседания детрита | 0,0019 | |
| SVS | Скорость оседания (для Scenedesmus) | 0,19 | |
| Температурный коэффициент минерализации обменного фосфора донных отложений | 1,03 | ||
| Максимальная удельная скорость поглощения углерода | 0,55 | ||
| Максимальная удельная скорость поглощения азота | 0,015 | ||
| Максимальная удельная скорость поглощения фосфора | 0,0014 | ||
| Минимальное и максимальное относительное содержание углерода в клетках фитопланктона | 0,15; 0,60 | - | |
| Минимальное и максимальное относительное содержание азота в клетках фитопланктона | 0,015; 0,10 | - | |
| Минимальное и максимальное относительное содержание фосфора в клетках фитопланктона | 0,001; 0,013 | - | |
| V | Объем воды в водоеме | m3 | |
| Y | Эффективность выедания зоопланктона рыбами | 0,63 | - |
| L | 0,59 | - | |
| Температурный коэффициент для разложения детрита | 1,072 | - |
Модель представлена системой дифференциальных уравнений.
Уровень I - дифференциальные уравнения:
![]() ; (1)
; (1)
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() ; (4)
; (4)
![]() ; (5)
; (5)
![]() ; (6)
; (6)
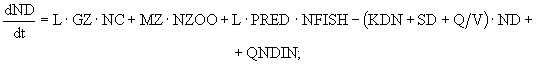 (7)
(7)
![]() ; (8)
; (8)
 (9)
(9)
![]() ; (10)
; (10)
![]() ; (11)
; (11)
![]() ; (12)
; (12)
![]() ; (13)
; (13)
![]() ; (14)
; (14)
![]() ; (15)
; (15)
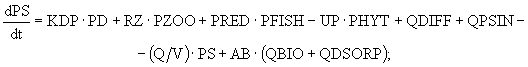 (16)
(16)
![]() . (17)
. (17)
Уровень II - скорости процессов:
![]() ; (18)
; (18)
![]() ; (19)
; (19)
![]() ; (20)
; (20)
![]() ; (21)
; (21)
![]() ; (22)
; (22)
![]() ; (23)
; (23)
![]() ; (24)
; (24)
![]() ; (25)
; (25)
![]() ; (26)
; (26)
![]() ; (27)
; (27)
![]() ; (28)
; (28)
![]() ; (29)
; (29)
![]() ; (30)
; (30)
![]() ; (31)
; (31)
![]() ; (32)
; (32)
![]() ; (33)
; (33)
![]() ; (34)
; (34)
![]() ; (35)
; (35)
![]() . (36)
. (36)
Уровень III - лимитирующие факторы:
![]() ; (37)
; (37)
![]() ; (38)
; (38)
![]() ; (39)
; (39)
![]() ; (40)
; (40)
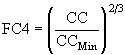 ; (41)
; (41)
![]() ; (42)
; (42)
![]() ; (43)
; (43)
![]() ; (44)
; (44)
![]() ; (45)
; (45)
![]() ; (46)
; (46)
![]() ; (47)
; (47)
![]() ; (48)
; (48)
![]() ; (49)
; (49)
![]() ; (50)
; (50)
![]() ;
; ![]() ;
; ![]() ; (51)
; (51)
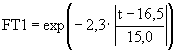 ; (52)
; (52)
![]() ; (53)
; (53)
![]() ; (54)
; (54)
![]() ; (55)
; (55)
![]() ; (56)
; (56)
![]() ; (57)
; (57)
![]() ; (58)
; (58)
![]() . (59)
. (59)
Уровень IV - вспомогательные уравнения:
![]() ; (60)
; (60)
![]() ; (61)
; (61)
![]() ; (62)
; (62)
![]() ; (63)
; (63)
![]() ; (64)
; (64)
![]() ; (65)
; (65)
![]() ; (66)
; (66)
![]() ; (67)
; (67)
![]() ; (68)
; (68)
![]() ; (69)
; (69)
![]() ; (70)
; (70)
![]() ; (71)
; (71)
![]() . (72)
. (72)
В то время как математическому моделированию процессов продуцирования фитопланктона посвящено большое число публикаций, имеется лишь несколько математических моделей для описания динамики биомассы водных макрофитов (Беляев и др., 1977; Курченко, Корелякова, 1979; Кравчук, Сиренко, 1984; Беляев, 1987; Экосистема озера Плещеево, 1989; Asaeda, Van Bon, 1997). В работе В.И. Беляева с соавторами (Беляев и др., 1977) предложена и исследована достаточно общая модель сообщества макрофитов в прибрежной морской экосистеме, представляющая собой систему интегро-дифференциальных уравнений. С помощью модели изучено влияние концентрации углекислоты в воде и коэффициента роста макрофитов на их биомассу, а также исследованы колебания фазовых переменных относительно стационарных состояний системы. В модели предполагается, что в результате перемешивания воды каждая особь равномерно засевает своими спорами свободное пространство, а численность потомства не зависит от численности родительских особей. Как известно, у многолетних корневищных растений вегетативное размножение доминирует. В отличие от этой модели, в модели Т.С. Курченко и И.Л. Кореляковой (Курченко, Корелякова, 1979) учитывается вегетативное размножение. Из факторов среды учитывалась освещенность, глубина мелководья и характер грунта. Предполагалось также, что пятно сообщества состоит из особей одного вида и его питание не лимитируется. Как обычно, при составлении математических моделей процессы роста, размножения, опада и отмирания рассматриваются осредненно относительно всех особей пятна, то есть считаются непрерывными. Авторами показано, что при определенных условиях наибольшая биомасса на 1 м2 может быть или на береговой линии водоема или в точке, лежащей между береговой и водной границами пятна сообщества. Интересная модель зарастания мелководий предложена Т.С. Кравчуком и И.П. Сиренко (Кравчук, Сиренко, 1984), с помощью которой можно одновременно описать как динамику биомассы макрофитов, так и определить закон изменения пятна сообщества. Как и в предыдущей модели, в ней учтены процессы фотосинтеза, размножения, отмирания, частичного выедания макрофитов хищниками, внутривидовой конкуренции. Однако, данная модель - одномерная и граница пятна сообщества движется только в одном направлении. Предложенный подход может быть применен при решении других задач экологии, например, в задачах занятия ареала особями одного вида, для описания процессов формирования и распространения "пятен цветения" водорослей.
В модели экосистемы озера Плещеево (Экосистема озера Плещеево, 1989) озеро разделено на 7 относительно однородных сегментов. Пять из них характеризуют литоральную зону, а два - глубоководную. Разделение литоральной зоны проведено в соответствии с характером зарастания участков макрофитами и особенностями поступления биогенных элементов с водосборного бассейна. Границей раздела сегментов глубоководной зоны служит термоклин, который разделяет ее на два сегмента - эпилимнион и гиполимнион. В каждом из 7 сегментов предполагалась пространственная однородность характеристик экосистемы. Точечные модели сегментов объединялись в единую сегментную сеть при помощи специального блока перемешивания, в котором концентрации компонентов экосистемы пересчитываются с учетом водообмена между сегментами и обмена с водосборным бассейном.
Уравнение модели построены на тех же принципах, что и модели, приведенные в работах (Воинов и др., 1985; Svirezhev et al., 1984). Выделены следующие агрегированные переменные: 1) R - рыбы (относятся к 16 видам из 6 семейств). В основном это мелкие рыбы. В их рационе преобладает зоопланктон. Альтернативным источником питания для них является детрит; 2) Z - зоопланктон (128 видов) - преобладают мирные ракообразные; 3) водоросли соответственно синезеленые A1, диатомовые A2 и пирофитовые PF. Они определяют почти всю продукцию фитопланктона. Выделение трех переменных позволяет описать смену фитоценозов в течение вегетационного периода; 4) макрофиты, соответственно погруженные WSи полупогруженные WE; 5) B - бактериальная микрофлора. Предполагается, что основная часть ее приходится на гетеротрофные микроорганизмы, осуществляющие деструкцию органических веществ; 6) POW - органический фосфор в воде; 7) PIW - минеральный фосфор в воде; 8) PDS - органический фосфор в донных отложениях; 9) PIS - минеральный фосфор в донных отложениях; 10) AOW - органический азот в воде; 11) AIW - минеральный азот в воде; 12) ADS - органический азот в донных отложениях; 13) AIS - минеральный азот в донных отложениях; 14) PE - фосфор в корнях полупогруженных макрофитов; 15) AE - азот в корнях полупогруженных макрофитов; 16) PS - фосфор в клетках погруженных макрофитов; 17) AS - азот в клетках погруженных макрофитов; 18) растворенный в воде кислород O2.
Отдельно учитывая специфику обмена, оба сегмента глубоководной зоны можно описывать в рамках "литоральной" модели, в которой гиполимнион выступает в роли дна. При этом соответствующие донные переменные преобразуются в PIH, PDH, AIH, ADH - минеральный и органический фосфор и азот в гиполиминионе. Кроме того, добавляется переменная O2H, характеризующая растворенный кислород в гиполиминионе.
Таким образом, модель литоральной зоны (сегменты 1 - 5) включает 21 переменную. Из них 6 связаны с писанием процессов на дне, а остальные 15 - с процессами в воде. В модель глубоководной зоны входят 16 переменных: 11 переменных для описания процессов в эпилимнионе (сегмент 6) и 5 - в гиполимнионе (сегмент 7).
Краткое математическое описание основных процессов, существенных для экосистемы озера Плещеево.
Фитопланктон.
Приращение биомассы фитопланктона осуществляется в процессе фотосинтеза и лимитируется биогенными элементами, светом и температурой. При этом предполагается мультипликативное влияние факторов среды и биогенного питания. Последнее определяется по правилу Либиха. Скорость роста биомассы водорослей задается в виде
![]() , (1)
, (1)
где i = A1, A2, PF; CP, CN и CC - стехиометрические коэффициенты, которые определяют соотношение фосфора, азота и углерода в биоте - P:N:C = CP:CN:CC; ![]() - коэффициент метаболизма, характеризующий долю потерь при росте водорослей; CCC = CP+CN+CC.
- коэффициент метаболизма, характеризующий долю потерь при росте водорослей; CCC = CP+CN+CC.
Функции ![]() и
и ![]() задают скорости потребления фосфора и азота соответственно. Предполагается, что они имеют S-образный вид и описываются выражением
задают скорости потребления фосфора и азота соответственно. Предполагается, что они имеют S-образный вид и описываются выражением
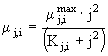 , (2)
, (2)
где j = PIWили AIW, ![]() - коэффициент максимальной скорости потребления j-го вещества,
- коэффициент максимальной скорости потребления j-го вещества, ![]() - коэффициент полунасыщения при потреблении j-го вещества.
- коэффициент полунасыщения при потреблении j-го вещества.
Функция ![]() описывает лимитирование роста биомассы температурой:
описывает лимитирование роста биомассы температурой:
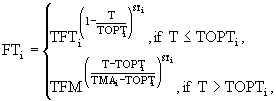 (3)
(3)
где ![]() - оптимальная для i-ой группы гидробионтов температура,
- оптимальная для i-ой группы гидробионтов температура, ![]() - максимальная для i-ой группы температура,
- максимальная для i-ой группы температура, ![]() - коэффициент скорости роста i-ой группы при температуре 0°С, Т - текущее значение температуры воды, TFM - значение температурной поправки при
- коэффициент скорости роста i-ой группы при температуре 0°С, Т - текущее значение температуры воды, TFM - значение температурной поправки при ![]() ,
, ![]() - коэффициент крутизны кривой.
- коэффициент крутизны кривой.
Кривая ![]() представляет собой функцию лимитирования светом и задается функцией Ди Торо, которая характеризует интегральную зависимость фотосинтеза в слое воды толщиной Н от суммарной солнечной радиации I на поверхности:
представляет собой функцию лимитирования светом и задается функцией Ди Торо, которая характеризует интегральную зависимость фотосинтеза в слое воды толщиной Н от суммарной солнечной радиации I на поверхности:
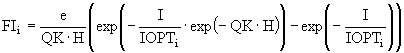 , (4)
, (4)
где ![]() - оптимальная для i-ой группы освещенность,
- оптимальная для i-ой группы освещенность, ![]() , CW, CA, CD - коэффициенты ослабления света соответственно чистой водой, взвешенными водорослями и детритом.
, CW, CA, CD - коэффициенты ослабления света соответственно чистой водой, взвешенными водорослями и детритом.
Убыль биомассы фитопланктона происходит за счет его выедания зоопланктоном и рыбами, а также за счет его естественной смертности и автолиза, которые задаются линейными функциями вида:
![]() ,
, ![]() . (5)
. (5)
Окончательное выражение для описания динамики биомассы i-го вида фитопланктона можно представить следующим дифференциальным уравнением:
![]() . (6)
. (6)
Член ![]() характеризует скорость выедания водорослей на других трофических уровнях.
характеризует скорость выедания водорослей на других трофических уровнях.
Уравнения для различных групп водорослей отличаются значениями коэффициентов трофических и лимитирующий функций. Способность синезеленых водорослей фиксировать молекулярный азот лимитируется этим элементом. Поэтому соответствующая функция роста ![]() определяется функцией, задающей скорость потребления биогенов при фосфорном лимитировании. Кроме того, синезеленые в меньшей степени потребляются представителями других трофических уровней, что отражено в значениях соответствующих коэффициентов.
определяется функцией, задающей скорость потребления биогенов при фосфорном лимитировании. Кроме того, синезеленые в меньшей степени потребляются представителями других трофических уровней, что отражено в значениях соответствующих коэффициентов.
Зоопланктон.
Зоопланктон питается фитопланктоном, бактериями и детритом. Процесс потребления их характеризуется такими же S-образными трофическими функциями, как и у фитопланктона:
![]() , (7)
, (7)
где вместо k может быть A1, A2, PF, B, POWили AOW; ![]() - коэффициент максимальной скорости потребления,
- коэффициент максимальной скорости потребления, ![]() - соответствующий коэффициент полунасыщения.
- соответствующий коэффициент полунасыщения.
Для поддержания стехиометрического соотношения в биомассе зоопланктона потребление фосфора и азота синхронизировано и задается формулой
![]() . (8)
. (8)
В итоге прирост биомассы зоопланктона описывается следующим выражением:
![]() (9)
(9)
где FTZ - температурная функция, описанная выше, TBZ - коэффициент метаболизма ![]() .
.
Убыль биомассы зоопланктона происходит за счет естественной смертности, самолимитирования и выедания рыбами. Смертность задается линейной функцией ![]() , а самолимитирование - квадратичной:
, а самолимитирование - квадратичной: ![]() , где ZMOR - коэффициент смертности, а ZMORR - коэффициент самолимитирования. Процесс выедания зоопланктона рыбами формализован в следующем пункте.
, где ZMOR - коэффициент смертности, а ZMORR - коэффициент самолимитирования. Процесс выедания зоопланктона рыбами формализован в следующем пункте.
Рыбы.
Основную биомассу рыб определяет численность уклеи, плотвы и молоди окуня. Поэтому при описании роста "агрегированной рыбы" за основу взят рацион именно этих видов рыб. В этой связи излюбленным кормом для рыб принят зоопланктон. Предусмотрена также возможность перехода их на питание фитопланктоном и детритом вместе с бактериями. При описании смертности рыб учитывается возможность заморных явлений при пониженных концентрациях растворенного кислорода. Предполагается также, что естественная смертность рыб может зависеть от температуры. Учитывается самолимитирование рыб путем выедания одних видов другими.
Прирост биомассы рыб характеризуется следующим выражением:
![]() , (10)
, (10)
где FTR - функция температурного лимитирования, S - функция, описывающая питание рыб с переключением, TBR - коэффициент метаболизма.
Рассмотри процесс переключения питания подробнее. Пусть ZKR - концентрация зоопланктона, при которой происходит переключение на заменяющий корм. Тогда ![]() , где
, где
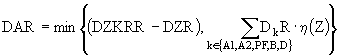 . (11)
. (11)
Здесь ![]() , DZR - трофические функции вида (2), причем функция DDR задается аналогично функции (8) для зоопланктона; DZKRRопределяется как значение функции DZRпри подстановке в нее значения ZKR вместо Z. Функция
, DZR - трофические функции вида (2), причем функция DDR задается аналогично функции (8) для зоопланктона; DZKRRопределяется как значение функции DZRпри подстановке в нее значения ZKR вместо Z. Функция ![]() характеризует вероятность перехода на заменяющий корм, которая, очевидно, зависит от концентрации излюбленного корма в среде.
характеризует вероятность перехода на заменяющий корм, которая, очевидно, зависит от концентрации излюбленного корма в среде.
Таким образом, прибавка за счет потребления заменяющего корма (DAR) не может сделать скорость роста выше той, что была при достаточном количестве излюбленного корма (Z > ZKR). Если ![]() , то реальные потоки заменяющих кормов устанавливаются пропорционально их потенциальным потокам:
, то реальные потоки заменяющих кормов устанавливаются пропорционально их потенциальным потокам:
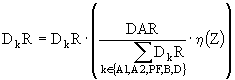 . (12)
. (12)
При описании смертности рыб учитывается возможность заморных явлений при пониженных концентрациях растворенного кислорода. Для этого используется функция FOR следующего вида:
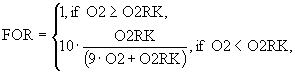 (13)
(13)
где O2RK - концентрация кислорода, соответствующая заморным условиям. Предполагается также, что естественная смертность рыб может зависеть от температуры. Температурная функция смертности задается в следующем виде:
![]() , (14)
, (14)
где TOPR - оптимальная температура для рыб, CMRT - коэффициент, характеризующий увеличение смертности при температуре 0°С относительно смертности при ![]() . Таким образом, смертность рыб описывается выражением
. Таким образом, смертность рыб описывается выражением ![]() , где RMOR - коэффициент смертности рыб. Для учета самолимитирования рыб путем выедания одних видов другими вводится квадратичный член вида
, где RMOR - коэффициент смертности рыб. Для учета самолимитирования рыб путем выедания одних видов другими вводится квадратичный член вида ![]() , где RMORR - коэффициент самолимитирования. Окончательное уравнение для описания временной динамики рыб имеет следующий вид:
, где RMORR - коэффициент самолимитирования. Окончательное уравнение для описания временной динамики рыб имеет следующий вид:
![]() . (15)
. (15)
Полупогруженные макрофиты.
Полупогруженные макрофиты характеризуются тремя фазовыми переменными. Одна из них описывает биомассу "надземной части" водных растений, две другие - азот и фосфор, содержащиеся в корнях. Такая детализация необходима для учета процесса запасания биогенов в корневищах в конце вегетационного периода перед отмиранием "надземной части" растений, то есть листьев и стеблей. Рост полупогруженных макрофитов рассматривается как двухступенчатый процесс. На первой стадии происходит потребление доступных биогенных элементов и накопление их в корнях. Так, для азота, содержащегося в корнях, соответствующий член имеет вид:
![]() , (16)
, (16)
где DAISAE - трофическая функция S-образного вида, FTAE - температурная функция, FIWE - функция лимитирования светом, которая будет описана ниже. Аналогичный вид имеет функция DPE, выражающая запас фосфора в корнях. Процесс отмирания корней описывается линейными функциями
![]() ,
, ![]() , (17)
, (17)
где PAEMOR - коэффициент отмирания корней.
Вторая стадия развития этих макрофитов характеризует рост самих растений, при котором используются биогенные вещества, накопленные в корнях. При концентрациях биогенных элементов в воде, превышающих некоторые пороговые значения, полупогруженные макрофиты могут потреблять биогены непосредственно из воды. Поэтому общее выражение для их роста имеет следующий вид:
![]() , (18)
, (18)
где TBWE - коэффициент метаболизма, FIWE - температурная функция, EMWE - емкость среды для полупогруженных макрофитов. Функция DWEIописывает потребление биогенных элементов из воды и имеет следующий вид:
![]() , (19)
, (19)
где
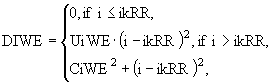 (20)
(20)
для i = PIW или i = AIW.
Величина ![]() характеризует биомассу корней. Функция
характеризует биомассу корней. Функция ![]() задает процесс потребления биогенных элементов, накопленных в корнях. Функции DPEWEи DAEWEимеет S-образный вид.
задает процесс потребления биогенных элементов, накопленных в корнях. Функции DPEWEи DAEWEимеет S-образный вид.
При описании роста полупогруженных макрофитов учитывается период их подводного развития. При этом считается, что оно начинается на некоторой глубине ![]() . Биомасса к моменту выходу растения из воды равна WEKR. Освещенность растений в период их подводного развития можно описать формулой
. Биомасса к моменту выходу растения из воды равна WEKR. Освещенность растений в период их подводного развития можно описать формулой ![]() , где
, где ![]() , QK - коэффициент поглощения света, определенный выше. Тогда, взяв за основу функцию Стила, зададим функцию освещенности в следующем виде:
, QK - коэффициент поглощения света, определенный выше. Тогда, взяв за основу функцию Стила, зададим функцию освещенности в следующем виде:
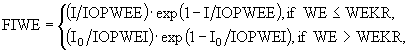 (21)
(21)
где IOPWEE - оптимальная освещенность на подводной стадии развития, IOPWEI - то же при выходе на поверхность.
Особого описания требует процесс перекачки биогенных веществ в корни в конце вегетационного периода. Предполагается, что этот механизм запускается при неблагоприятных условиях (слишком высокой или слишком низкой температуре воды). Соответствующая функция задается формулой:
![]() (22)
(22)
где TWEP1, TWEP2 - пороговые температуры, CTMP - коэффициент, характеризующий скорость перекачки. Тогда процесс перекачки будет определяться выражением ![]() . При этом доли накопления азота и фосфора в корнях будут соответственно равны
. При этом доли накопления азота и фосфора в корнях будут соответственно равны ![]() и
и ![]() . Температурная функция отмирания макрофитов имеет такой же вид, как и функция FTMR. Процесс захоронения биогенных веществ при переходе к неблагоприятным условиям предшествует массовому отмиранию растений. В целом процесс отмирания задается функцией
. Температурная функция отмирания макрофитов имеет такой же вид, как и функция FTMR. Процесс захоронения биогенных веществ при переходе к неблагоприятным условиям предшествует массовому отмиранию растений. В целом процесс отмирания задается функцией ![]() , где WEMOR - коэффициент смертности.
, где WEMOR - коэффициент смертности.
В итоге динамику полупогруженных макрофитов мы можем описать следующей системой уравнений:
![]() , (23)
, (23)
![]() , (24)
, (24)
![]() , (25)
, (25)
где ![]() .
.
Погруженные макрофиты.
Описание роста погруженных макрофитов схоже с описанием роста полупогруженных макрофитов, но в данном случае учитывается накопление биогенных элементов не в корнях, а в клетках растений, и поэтому в роли переменных в модели участвует не только биомасса погруженных макрофитов, но и накопленные в клетках азот и фосфор. Полагая, что основную часть минерального питания погруженные макрофиты получают из толщи воды, а пренебрежимо малую - через корни, потребление биогенных элементов клетками можно задать следующей формулой:
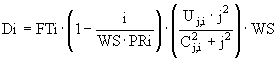 , (26)
, (26)
где i = ASили PS, а j = AIWили PIWсоответственно, ![]() - максимальная скорость потребления,
- максимальная скорость потребления, ![]() - коэффициент полунасыщения, FTi - температурная функция, PRi - максимально возможная доля соответствующего биогенного вещества в клетках растения. Накопленные в клетках элементы используются для построения биомассы растений:
- коэффициент полунасыщения, FTi - температурная функция, PRi - максимально возможная доля соответствующего биогенного вещества в клетках растения. Накопленные в клетках элементы используются для построения биомассы растений:
![]() , (27)
, (27)
где ![]() , DPSWS, DASWS - S-образные трофические функции, FTWS - температурная функция, FIWS - функция освещенности такого же вида, как и для фитопланктона, TBWS - коэффициент метаболизма, EMWS - емкость среды.
, DPSWS, DASWS - S-образные трофические функции, FTWS - температурная функция, FIWS - функция освещенности такого же вида, как и для фитопланктона, TBWS - коэффициент метаболизма, EMWS - емкость среды.
Убыль биомассы рассматриваемых макрофитов происходит за счет их смертности согласно зависимости: ![]() , где WSMOR - коэффициент смертности. При этом накопленные в клетках биогенные элементы возвращаются в воду в количествах
, где WSMOR - коэффициент смертности. При этом накопленные в клетках биогенные элементы возвращаются в воду в количествах ![]() ,
, ![]() .
.
Бактерии.
Описание развития бактерий является одним из наиболее спорных моментов при формализации экосистемы водоема. С одной стороны, огромное многообразие микроорганизмов играет важную роль на разных этапах круговорота вещества в водоеме, с другой, имеющиеся экспериментальные данные позволяют учесть все разновидности бактерий лишь в виде одной агрегированной переменной. В данной модели под бактериями понимается обширный класс микроорганизмов-деструкторов. Действие этих микроорганизмов во многом представляется аналогичным действию ферментов, с той лишь разницей, что часть субстрата идет на удовлетворение собственных потребностей бактерий. При этом учитываются влияние температуры, кислородные условия (в аэробных условиях интенсивность бактериальной деструкции выше, чем в анаэробных). Конечными продуктами бактериального разложения являются неорганический азот и фосфор. Рассматривается переработка субстрата, при этом k-ая доля идет на построение биомассы бактерий, а (1-k)-ая доля потока переходит в продукт. Интенсивность переработки субстрата определяется биомассой бактерий, прирост которой задается в следующем виде:
![]() , (28)
, (28)
где ![]() - температурная функция, являющаяся аналогом функции Вант-Гоффа,
- температурная функция, являющаяся аналогом функции Вант-Гоффа, ![]() - температура, при которой измерены прочие коэффициенты уравнения, FOB - кислородная функция, отражающая тот факт, что в аэробных условиях интенсивность бактериальной деструкции выше, чем в анаэробных.
- температура, при которой измерены прочие коэффициенты уравнения, FOB - кислородная функция, отражающая тот факт, что в аэробных условиях интенсивность бактериальной деструкции выше, чем в анаэробных.
Конечными продуктами бактериального разложения являются PIWи AIW. Убыль биомассы бактерий происходит за счет естественной смертности, выедания их зоопланктоном и рыбами и описывается так же, как смертность и выедание фитопланктона. Следует отметить, что предложенная здесь формализация бактериальных процессов является весьма приближенной, однако уже ее достаточно для того, чтобы учесть вклад бактерий в общий круговорот вещества в экосистеме.
Детрит.
Детрит в модели описывается четырьмя переменными, характеризующими концентрации органического азота и фосфора в детрите воды и в активном слое донных отложений (ДО) - в случае литорали, в гиполимнионе - в случае пелагиали. Считается, что основным источником поступления ОВ в воду являются отмершие гидробионты, а содержание азота и фосфора в детрите находится в соответствие с законами стехиометрии. Другим источником поступления ОВ, который также необходимо учитывать, является обмен воды с дном за счет турбулентной диффузии. Для описания этого процесса используется простейшее выражение следующего вида:
![]() , (29)
, (29)
где COFDPO - коэффициент турбулентной диффузии, зависящий от скорости ветра. Ясно, что этот процесс может работать как в одну, так и в другую сторону. Но, как правило, накопление детрита на дне идет, в основном, за счет седиментации, которую можно описать следующим образом:
![]() , (30)
, (30)
где COSP - коэффициент седиментации. Выражения для AOWи ADS записываются аналогично.
Взвешенное в воде органическое вещество подвергается бактериальному разложению, его потребляют зоопланктон и рыбы. Предполагается, что численность бактерий на дне и в гиполимнионе не может лимитировать скорость деструкции органического вещества DS. Это позволяет представить последнюю линейной функцией:
![]() , (31)
, (31)
где CPDPI - коэффициент деструкции, FOB - кислородная функция (такая же, как и для бактерий). Вид аргумента этой функции отражает тот факт, что кислород на дне меньше, чем в толще воды на некоторую величину OS.
Считается, что некоторая доля детрита, равная ![]() , выходит из активного слоя и откладывается в ДО. Отмирающие корни полупогруженных макрофитов переходят непосредственно в детрит дна PDSи ADS.
, выходит из активного слоя и откладывается в ДО. Отмирающие корни полупогруженных макрофитов переходят непосредственно в детрит дна PDSи ADS.
Биогенные элементы.
Доступные для первичных продуцентов неорганические вещества представлены четырьмя переменными: азотом и фосфором, растворенными в воде, азотом и фосфором в седиментах. При описании обмена фосфором между толщей воды и седиментами за счет турбулентной диффузии используется следующая формула: ![]() , где COFDPI - коэффициент турбулентной диффузии, PIWKR - концентрация насыщения для растворенного неорганического фосфора. Аналогичный вид имеет формула и для обмена минеральным азотом AIW.
, где COFDPI - коэффициент турбулентной диффузии, PIWKR - концентрация насыщения для растворенного неорганического фосфора. Аналогичный вид имеет формула и для обмена минеральным азотом AIW.
В анаэробных условиях, как известно, может происходить интенсивное обогащение воды фосфором за счет PIS. Этот процесс формализуется заданием зависимости концентрации насыщения PIWKR от концентрации растворенного кислорода. При этом концентрация насыщения в анаэробных условиях значительно превосходит концентрацию насыщения для PIW в аэробных условиях.
Для озера Плещеево основными источниками биогенных элементов автохтонного происхождения являются разложение мертвого органического вещества и растворение некоторой части метаболитов гидробионтами. Модель учитывает также, что определенная часть биогенных веществ седиментов может захороняться в донных отложениях, выпадая из общего круговорота веществ.
Кислород.
Пополнение запасов кислорода идет за счет фотосинтеза и аэрации водной толщи. Считается, что фотосинтез пропорционален скорости роста первичных продуцентов с постоянным для каждой группы коэффициентом ассимиляции. Процесс реаэрации описывается следующей упрощенной формулой: ![]() , где O2AIR - концентрация насыщения растворенным кислородом, а CREAR - коэффициент реаэрации, являющийся функцией скорости ветра. Кислород расходуется в основном на окисление мертвого органического вещества в воде и седиментах, на дыхание гидробионтов, которое считается пропорциональным биомассам соответствующих групп организмов.
, где O2AIR - концентрация насыщения растворенным кислородом, а CREAR - коэффициент реаэрации, являющийся функцией скорости ветра. Кислород расходуется в основном на окисление мертвого органического вещества в воде и седиментах, на дыхание гидробионтов, которое считается пропорциональным биомассам соответствующих групп организмов.
Гидродинамический блок.
Гидродинамический блок предназначен для описания формирования течений в озере и связанного с ними переноса растворенных и взвешенных веществ по акватории. В его основу положена хорошо известная модель стационарный ветровых течений (Фельзенбаум, 1960). С помощью гидродинамического блока определены перетоки воды между отдельными сегментами, на которые было разделено озеро.
Оценку параметров модели проводили вначале по литературным данным. Это позволило определить интервалы возможного их изменения. Затем была произведена оценка чувствительности модели к возмущениям параметров, внешних функций и начальных данных. Было отмечено, что наибольшая чувствительность наблюдалась к параметрам, характеризующим максимальные скорости роста и смертности организмов. В следующую по важности группу вошли параметры, представляющие собой оптимальную температуру, степень крутизны температурной кривой, оптимальную освещенность, коэффициенты седиментации и диффузии. Верификация модели заключалась в проведении расчетов при фиксированных значениях параметров, найденных на этапе настройки, но при изменении значений внешних функций (климатических факторов, притока, оттока, биогенной нагрузки) или на массиве независимых данных, которые не были задействованы при настройке. При отсутствии достаточного количества экспериментальных данных особо большое значение приобретает тщательный анализ области устойчивости модели и определение критических режимов функционирования экосистемы. Анализ показал, что разработанная модель является грубой как относительно ее параметров, так и внешних функций. Области ее устойчивости хватает для изучения самых разнообразных режимов функционирования экосистемы.
В работе (Asaeda, Van Bon, 1997) рассматривается имитационная модель эвтрофикации мелководного озера. Особенностью данной модели является совместное рассмотрение не только динамики фитопланктона и биогенных элементов в воде, но также динамики погруженных макрофитов и биогенных элементов в седиментах. С помощью этой модели исследовался вопрос о возможном влиянии макрофитов на цветение фитопланктона в озерах. Модель построена по модульному принципу. Первый модуль описывает развитие фитопланктона, динамику биогенных элементов в воде. Второй модуль рассматривает процессы обмена биогенов между водой и верхним слоем донных отложений. Третий модуль предназначен для моделирования развития прикрепленных макрофитов.
Модуль I. Динамика фитопланктона и биогенных элементов в воде.
В данной блоке модели рассматривается три вида фитопланктона: диатомовые, зеленые и синезеленые. В качестве индикатора биомассы фитопланктона рассматривается концентрация хлорофилла "а". Для описания светового лимитирования роста фитопланктона используется функция Стила. Учтено биогенное лимитирование и влияние температурных условий на развитие планктона. Конкуренция между фитопланктоном и прикрепленными макрофитами за свет описывается в модели через коэффициент экстинкции.
Предполагается, что динамика фитопланктона определяется процессами
·роста;
·дыхания;
·естественной смертности;
·оседания;
·выедания зоопланктоном.
Предполагается, что поглощение азота и фосфора изменяется в соответствии с изменениями концентраций данных биогенных элементов в воде. Процесс поглощения биогенов прекращается после того, как будет достигнут некоторый установленный предел внутриклеточного их содержания.
Уменьшение количества биогенных элементов в клетках фитопланктона связано с процессами
·дыхания;
·экскреции;
·смертности;
·выедания зоопланктоном;
·оседанием.
Процессы изменения хлорофилла "а" ![]() и внутриклеточного содержания азота
и внутриклеточного содержания азота ![]() и фосфора
и фосфора ![]() у различных групп фитопланктона описаны в модели следующими дифференциальными уравнениями:
у различных групп фитопланктона описаны в модели следующими дифференциальными уравнениями:
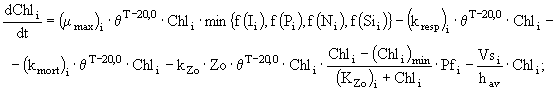 (1)
(1)
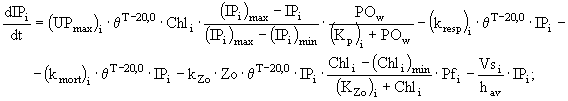 (2)
(2)
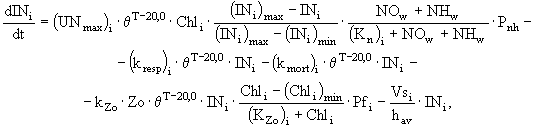 (3)
(3)
где ![]() - концентрация хлорофилла "а" в клетках диатомовых (i = 1), зеленых (i = 2) и синезеленых (i = 3) водорослей
- концентрация хлорофилла "а" в клетках диатомовых (i = 1), зеленых (i = 2) и синезеленых (i = 3) водорослей ![]() ;
; ![]() и
и ![]() - внутриклеточная концентрация фосфора и азота (Pmg или Nmg
- внутриклеточная концентрация фосфора и азота (Pmg или Nmg![]() ) с максимальными и минимальными значениями
) с максимальными и минимальными значениями ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() и
и ![]() - максимальные удельные скорости поглощения фосфора и азота соответственно
- максимальные удельные скорости поглощения фосфора и азота соответственно ![]() ;
; ![]() ,
, ![]() и
и ![]() - коэффициенты дыхания, смертности и выедания фитопланктона зоопланктоном
- коэффициенты дыхания, смертности и выедания фитопланктона зоопланктоном ![]() ; Zo - биомасса зоопланктона
; Zo - биомасса зоопланктона ![]() ;
; ![]() - минимальная концентрация хлорофилла "а" в клетках фитопланктона, при которой возможно выедание его зоопланктоном
- минимальная концентрация хлорофилла "а" в клетках фитопланктона, при которой возможно выедание его зоопланктоном ![]() ;
; ![]() - максимальная удельная скорость роста фитопланктона
- максимальная удельная скорость роста фитопланктона ![]() ;
; ![]() - эмпирический коэффициент в температурной функции;
- эмпирический коэффициент в температурной функции; ![]() и
и ![]() - константы полунасыщения по фосфору и азоту
- константы полунасыщения по фосфору и азоту ![]() ;
; ![]() - константа полунасыщения для выедания фитопланктона зоопланктоном
- константа полунасыщения для выедания фитопланктона зоопланктоном ![]() ;
; ![]() - скорости оседания диатомовых, зеленых и синезеленых водорослей соответственно;
- скорости оседания диатомовых, зеленых и синезеленых водорослей соответственно; ![]() - коэффициент пищевого предпочтения для различных видов водорослей; Т - температура воды (°С);
- коэффициент пищевого предпочтения для различных видов водорослей; Т - температура воды (°С); ![]() ,
, ![]() ,
, ![]() и
и ![]() - лимитирующие функции по условиям освещенности, фосфору, азоту и кремнию соответственно; t - время.
- лимитирующие функции по условиям освещенности, фосфору, азоту и кремнию соответственно; t - время.
В результате процессов
·дыхания;
·естественной смертности;
·выедания фитопланктона зоопланктоном;
·минерализации органических веществ;
·нитрификации;
·выделения биогенных элементов из донных отложений;
·поглощения их макрофитами
формируется запас биогенных элементов в воде.
Процессы изменения растворенных в воде фосфатов, аммонийного, нитратного азота и силикатов описываются в модели следующими дифференциальными уравнениями:
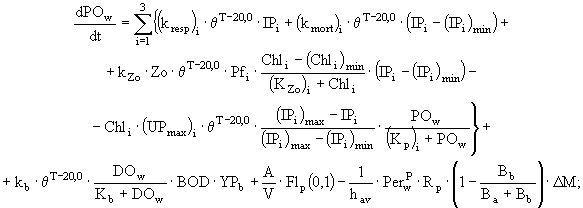 (4)
(4)
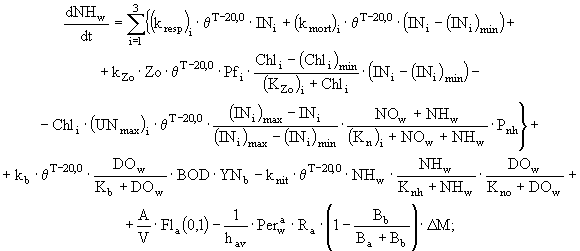 (5)
(5)
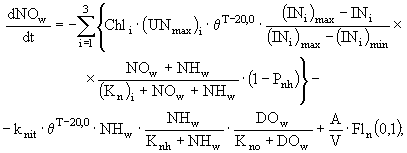 (6)
(6)
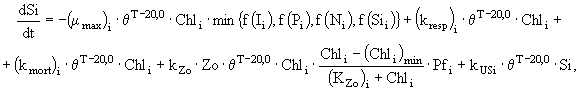 (7)
(7)
где ![]() ,
, ![]() ,
, ![]() и
и ![]() - концентрации растворенного в воде кислорода, фосфатов, нитратов, аммиачного азота;
- концентрации растворенного в воде кислорода, фосфатов, нитратов, аммиачного азота; ![]() и
и ![]() - концентрации соответственно химически активного и химически неактивного кремния
- концентрации соответственно химически активного и химически неактивного кремния ![]() ;
; ![]() ,
, ![]() и
и ![]() - потоки нитратного, аммонийного азота и фосфатов через поверхность раздела вода - донные отложения;
- потоки нитратного, аммонийного азота и фосфатов через поверхность раздела вода - донные отложения; ![]() - фактор предпочтения поглощения аммонийного азота;
- фактор предпочтения поглощения аммонийного азота; ![]() - коэффициент минерализации химически неактивного кремния;
- коэффициент минерализации химически неактивного кремния; ![]() и
и ![]() - отношения высвобождаемого фосфора и азота (mg) к кислороду, используемому на окисление органических веществ; BOD - биохимическое потребление кислорода
- отношения высвобождаемого фосфора и азота (mg) к кислороду, используемому на окисление органических веществ; BOD - биохимическое потребление кислорода ![]() ;
; ![]() ,
, ![]() и
и ![]() - соответствующие константы полунасыщения;
- соответствующие константы полунасыщения; ![]() - скорость процесса нитрификации при температуре 20°С;
- скорость процесса нитрификации при температуре 20°С; ![]() ,
, ![]() и
и ![]() ,
, ![]() - относительные вклады побегов и корней макрофитов в процессах поглощения ими фосфатов и аммонийного азота.
- относительные вклады побегов и корней макрофитов в процессах поглощения ими фосфатов и аммонийного азота.
Изменение концентрации растворенного в воде кислорода определяется процессами
·фотосинтеза;
·дыхания;
·смертности;
·биохимического окисления органических веществ;
·нитрификации;
·поглощения в донных отложениях;
·газообмена с атмосферой;
·жизнедеятельности макрофитов.
С учетом этого, динамика концентрации растворенного в воде кислорода и биохимического потребления кислорода задаются в модели следующими дифференциальными уравнениями:
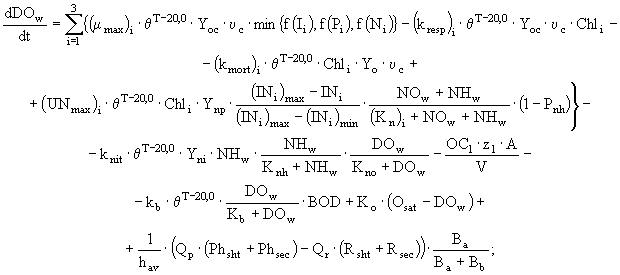 (8)
(8)
![]() (9)
(9)
где
![]() ; (10)
; (10)
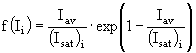 ;
; ![]() ; (11a,б)
; (11a,б)
![]() ;
; ![]() ; (11в,г)
; (11в,г)
![]() ;
; ![]() ;
; ![]() ; (12а-в)
; (12а-в)
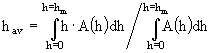 ; (13)
; (13)
![]() ;
; ![]() ; (14а,б)
; (14а,б)
![]() ;
; 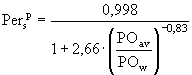 ; (15а,б)
; (15а,б)
![]() ;
; 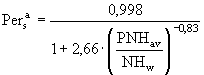 . (16а,б)
. (16а,б)
Здесь ![]() - скорость поглощения кислорода пограничным аэробным слоем донных отложений
- скорость поглощения кислорода пограничным аэробным слоем донных отложений ![]() ;
; ![]() - константа полунасыщения для поглощения аммонийного азота;
- константа полунасыщения для поглощения аммонийного азота; ![]() - концентрация кислорода при насыщении;
- концентрация кислорода при насыщении; ![]() - коэффициент обмена
- коэффициент обмена ![]() ;
; ![]() ,
, ![]() ,
, ![]() и
и ![]() - стехиометрические отношения кислорода к углероду для процессов фотосинтеза и дыхания, кислорода, используемого при разложении органического вещества фитопланктона в результате его отмирания, к углероду, кислорода к азоту в процессе трансформации нитратов и, наконец, кислорода к азоту для процесса нитрификации соответственно;
- стехиометрические отношения кислорода к углероду для процессов фотосинтеза и дыхания, кислорода, используемого при разложении органического вещества фитопланктона в результате его отмирания, к углероду, кислорода к азоту в процессе трансформации нитратов и, наконец, кислорода к азоту для процесса нитрификации соответственно; ![]() ,
, ![]() и
и ![]() - коэффициенты поглощения света водой
- коэффициенты поглощения света водой ![]() , клетками фитопланктона
, клетками фитопланктона ![]() и макрофитами
и макрофитами ![]() ;
; ![]() и
и ![]() - соответственно содержание азота и фосфора на единицу сухого веса макрофитов; M,
- соответственно содержание азота и фосфора на единицу сухого веса макрофитов; M, ![]() и
и ![]() - общая биомасса макрофитов, биомасса макрофитов выше и ниже границы раздела между водой и донными отложениями в единицах сухого веса
- общая биомасса макрофитов, биомасса макрофитов выше и ниже границы раздела между водой и донными отложениями в единицах сухого веса ![]() ;
; ![]() ,
, ![]() ,
, ![]() и
и ![]() - биомассы, связанные с фотосинтезом и тратами на дыхание соответственно для основных и вторичных побегов макрофитов;
- биомассы, связанные с фотосинтезом и тратами на дыхание соответственно для основных и вторичных побегов макрофитов; ![]() и
и ![]() - коэффициенты перехода от массы сухого веса к массе кислорода для процессов фотосинтеза и дыхания соответственно;
- коэффициенты перехода от массы сухого веса к массе кислорода для процессов фотосинтеза и дыхания соответственно; ![]() - средняя концентрация растворенных фосфатов в донных отложениях;
- средняя концентрация растворенных фосфатов в донных отложениях; ![]() ,
, ![]() ,
, ![]() и
и ![]() (i = 1, 2, 3, 4) - соответственно пористость, толщина слоев донных отложений, концентрации растворенных фосфатов и аммиачного азота в каждом из этих четырех слоев; I,
(i = 1, 2, 3, 4) - соответственно пористость, толщина слоев донных отложений, концентрации растворенных фосфатов и аммиачного азота в каждом из этих четырех слоев; I, ![]() и
и ![]() - фотосинтетически активная радиация, среднее значение ФАР и предельная ее интенсивность для i-го вида фитопланктона; h,
- фотосинтетически активная радиация, среднее значение ФАР и предельная ее интенсивность для i-го вида фитопланктона; h, ![]() и
и ![]() - текущая, максимальная и средняя глубины озера (m); А,
- текущая, максимальная и средняя глубины озера (m); А, ![]() и V - общая площадь донных отложений, площадь сечения водоема на глубине h и объем водоема соответственно.
и V - общая площадь донных отложений, площадь сечения водоема на глубине h и объем водоема соответственно.
Таким образом, в первом модуле модели используются 15 переменных состояния и 58 эмпирических параметров.
Модуль II. Процессы обмена биогенными элементами между водой и донными отложениями.
Основными процессами, которые определяют динамику биогенов в донных отложениях, являются:
·адвективный перенос, связанный с инфильтрацией;
·диффузия;
·биотурбация;
·седиментация.
Для математического описания этих процессов весь активный слой донных отложений был разделен на четыре подслоя: аэробный, слой денитрификации, верхний восстановленный и нижний восстановленный слои. Предполагается также, что над активным слоем существует тонкий пограничный слой обмена.
Таблица 1. Схема процессов биогенного обмена между водой и верхним слоем донных отложений.
| Layer | Detritus | Nitrate | Ammonium | Dissolved Oxygen | Phosphate | |
| Water column |
Settling ? Mineralization Degradation Humification Incorporation |
Denitrification Nitrification |
Ammonification Nitrification Absorption Dispersion |
Photosynthesis Oxydation BOD Reaeration Dispersion |
Mineralization Adsorption Dispersion | |
| Z0 |
Newly deposited detritus | Degradation |
Dispersion |
Ammonification | BOD |
Dispersion |
| Z1 |
Aerobic layer |
Degradation Incorporation |
Dispersion Nitrification Flux to denitrifying layer |
Dispersion Seepage Degradation Nitrification Seepage |
Oxydation Dispersion |
Dispersion Adsorption Seepage Mineralization Bioturbation |
| Z2 |
Denitrifying layer | Degradation Incorporation |
Dispersion Nitrification |
Degradation | Nitrification Oxydation |
Dispersion Adsorption |
| Z3 |
Upper reduced layer | Degaradation Bioturbation |
Nitrification Denitrification |
Dispersion Seepage |
Nitrification Deoxygenation |
Seepage Burial Mineralization Bioturbation Dispersion |
| Z4 | Lower reduced layer | Burial ? Degradation |
Dispersion Nitrification Denitrification |
Degradation | Deoxygenation | Seepage ? Burial ? Mineralization |
| Inactive bottom layer | Inactive |
Inactive |
Seepage ? |
Inactive |
Seepage ? Burial ? |
Толщина аэробного слоя и слоя денитрификации зависит от интенсивности процессов переноса кислорода и нитратов и соответствующих химических реакций в этих слоях. Толщина аэробного слоя задается в модели следующим уравнением:
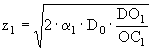 , (17)
, (17)
где ![]() - коэффициент турбулентной диффузии и биотурбации растворенного кислорода
- коэффициент турбулентной диффузии и биотурбации растворенного кислорода ![]() ,
, ![]() - концентрация растворенного кислорода в этом слое
- концентрация растворенного кислорода в этом слое ![]() . Толщина второго слоя, слоя денитрификации, определяется следующим уравнением:
. Толщина второго слоя, слоя денитрификации, определяется следующим уравнением:
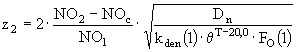 , (18)
, (18)
где ![]() - концентрация нитратов в i-ом слое
- концентрация нитратов в i-ом слое ![]() ;
; ![]() - критическая их концентрация
- критическая их концентрация ![]() ;
; ![]() - коэффициент турбулентной диффузии и биотурбации нитратов
- коэффициент турбулентной диффузии и биотурбации нитратов ![]() ;
; ![]() - скорость денитрификации в i-ом слое
- скорость денитрификации в i-ом слое ![]() ;
; ![]() - функция, учитывающая зависимость процесса денитрификации от концентрации растворенного кислорода. Эта функция задается следующим выражением:
- функция, учитывающая зависимость процесса денитрификации от концентрации растворенного кислорода. Эта функция задается следующим выражением:
![]() , (19)
, (19)
где ![]() - константа полунасыщения для кислородного лимитирования процесса денитрификации. Толщина верхнего восстановленного слоя принималась равной 2 см, а общая толщина химически активного слоя донных отложений - 20 см.
- константа полунасыщения для кислородного лимитирования процесса денитрификации. Толщина верхнего восстановленного слоя принималась равной 2 см, а общая толщина химически активного слоя донных отложений - 20 см.
Концентрация растворенного кислорода в каждом из четырех выделенных слоев с учетом
·вертикального его переноса между слоями;
·потребления при нитрификации;
·процессов окисления;
·выделения кислорода прикрепленными макрофитами
рассчитывается с помощью следующих балансовых уравнений:
![]() . (20)
. (20)
Потоки кислорода из слоя i в слой i + 1 определяются следующим образом:
![]() ;
; ![]() ;
;
![]() , (21)
, (21)
где ![]() ,
, ![]() - отношение концентраций растворенного кислорода в пограничном слое и придонном слое воды;
- отношение концентраций растворенного кислорода в пограничном слое и придонном слое воды; ![]() и
и ![]() - скорости поглощения и выделения кислорода прикрепленными макрофитами в слое i
- скорости поглощения и выделения кислорода прикрепленными макрофитами в слое i![]() .
.
Кислород поглощается в результате процессов разложения детрита, нитрификации и окисления различных веществ. Остающаяся часть кислорода или накапливается в седиментах или же выделяется обратно в воду в газообразном состоянии. В соответствие с этим, скорости потребления кислорода в каждом слое седиментов вычисляются в модели следующим образом:
![]() , (22)
, (22)
![]() , (23)
, (23)
![]() , (24)
, (24)
![]() , (25)
, (25)
где ![]() и
и ![]() - концентрации детрита соответственно в слое i и 0
- концентрации детрита соответственно в слое i и 0 ![]() ;
; ![]() - скорость разложения детрита в слое i
- скорость разложения детрита в слое i![]() ;
; ![]() - скорость нитрификации при 20°С в слое i
- скорость нитрификации при 20°С в слое i![]() ; fra - доля разлагаемых веществ, которые удаляются из данного слоя седиментов. Скорость разложения детрита ограничивается только концентрацией растворенного кислорода, в то время как скорость нитрификации - концентрациями кислорода и аммонийного азота. Эти ограничения учитываются через функции
; fra - доля разлагаемых веществ, которые удаляются из данного слоя седиментов. Скорость разложения детрита ограничивается только концентрацией растворенного кислорода, в то время как скорость нитрификации - концентрациями кислорода и аммонийного азота. Эти ограничения учитываются через функции ![]() и
и ![]() , где
, где ![]() - концентрация аммонийного азота в слое i
- концентрация аммонийного азота в слое i![]() ,
, ![]() - константа полунасыщения для кислородного лимитирования процесса разложения детрита
- константа полунасыщения для кислородного лимитирования процесса разложения детрита ![]() .
.
Скорость выделения кислорода прикрепленными макрофитами в каждом слое седиментов определяется процессами фотосинтеза и дыхания. Следовательно,
![]() , (26)
, (26)
где L - общая глубина проникновения корней макрофитов, ![]() - глубина ризосферы в i-ом слое седиментов.
- глубина ризосферы в i-ом слое седиментов.
Концентрация детрита в придонном слое воды определяется процессами
·смертности (главным образом, фитопланктона);
·оседанием мертвого фитопланктона;
·разложением фитопланктона.
С учетом этих процессов, можно составить систему балансовых уравнений, описывающих процесс изменений концентраций детрита в воде, на границе раздела вода - донные отложения и в каждом слое седиментов:
![]() ; (27)
; (27)
![]() ; (28)
; (28)
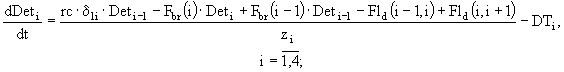 (29)
(29)
причем
![]() ;
; ![]() ;
; 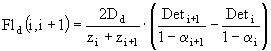 ;
; ![]() , (30а-г)
, (30а-г)
rc - скорость поступления детрита в донные отложения ![]() ; s - скорость седиментации детрита
; s - скорость седиментации детрита ![]() ;
; ![]() - символ Кронекера;
- символ Кронекера; ![]() - скорость захоронения детрита в донных отложениях
- скорость захоронения детрита в донных отложениях ![]() .
.
Концентрация нитратов в седиментах регулируется тремя процессами:
·вертикальным переносом между слоями;
·нитрификации;
·денитрификации.
Дифференциальное уравнение, определяющее временную динамику нитратов имеет следующий вид:
![]() . (31)
. (31)
Потоки нитратов между слоями задаются так:
![]() ;
; ![]() ;
;
![]() , (32а-в)
, (32а-в)
причем
![]() . (33)
. (33)
Концентрация аммонийного азота определяется процессами
·вертикального переноса;
·разложения детрита;
·нитрификации;
·поглощением его прикрепленными макрофитами.
Таким образом, дифференциальное уравнение, определяющее временную динамику аммонийного азота, имеет следующий вид:
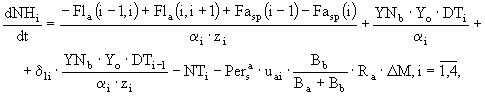 (34)
(34)
где ![]() - фильтрационный поток аммонийного азота между слоями
- фильтрационный поток аммонийного азота между слоями ![]() . Предполагается, что доля аммонийного азота, потребляемая макрофитами в каждом слое седиментов, равна
. Предполагается, что доля аммонийного азота, потребляемая макрофитами в каждом слое седиментов, равна
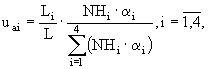 (35)
(35)
а потоки между слоями задаются в виде следующих соотношений:
![]() ;
; ![]() ;
;
![]() . (36а-в)
. (36а-в)
Неорганический фосфор фосфатов разделен в модели на три части: растворенный, адсорбированный и осажденный. В соответствии с этим:
![]() ,
, ![]() ,
, ![]() , (37)
, (37)
где ![]() - концентрация неорганического фосфора фосфатов в слое i,
- концентрация неорганического фосфора фосфатов в слое i, ![]() ,
, ![]() и
и ![]() - доли растворенной, адсорбированной и осажденной части в слое i, причем
- доли растворенной, адсорбированной и осажденной части в слое i, причем ![]() . Баланс неорганического фосфора фосфатов в каждом из выделенных слоев определяется следующим дифференциальным уравнением:
. Баланс неорганического фосфора фосфатов в каждом из выделенных слоев определяется следующим дифференциальным уравнением:
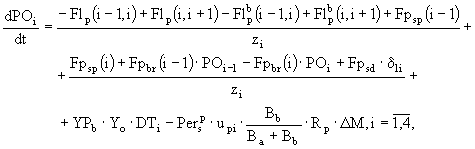 (38)
(38)
где потоки неорганического фосфора фосфатов между слоями задаются равенствами
![]() ;
; ![]() ;
;
![]() . (39а-в)
. (39а-в)
Потоки неорганического фосфора фосфатов, которые определяются процессами биотурбации, вычисляются в модели с помощи следующих соотношений:
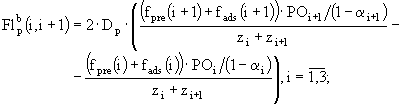
![]() . (40а,б)
. (40а,б)
Предполагается, что доля фосфора фосфатов, потребляемая макрофитами в каждом слое седиментов, равна
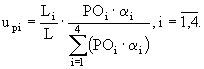 (41)
(41)
Во втором модуле модели используются 31 эмпирический параметр. Большинство из них оценены по литературным данным.
Модуль III. Описание динамики развития макрофитов.
В данном модуле рассматриваются пять переменных состояния: биомасса основных побегов, биомасса вторичных побегов, биомасса корневой системы макрофитов, биомасса клубеньков и биомасса вновь образующихся клубеньков. Все эти биомассы выражаются в единицах сухого веса.
Чистый прирост биомассы макрофитов обеспечивается следующими основными процессами:
·фотосинтезом;
·дыханием;
·отмиранием макрофитов;
·использованием некоторой части отмерших макрофитов в процессах роста;
·образованием вторичных побегов;
·образованием новых клубеньков.
В соответствии с этим, система дифференциальных уравнений, определяющая временную динамику выделенных агрегированных переменных блока макрофитов будет иметь следующий вид:
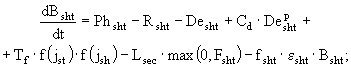 (42)
(42)
![]() ; (43)
; (43)
![]() ; (44)
; (44)
![]() ; (45)
; (45)
![]() , (46)
, (46)
причем
![]() , (47)
, (47)
![]() , (48)
, (48)
![]() , (49)
, (49)
![]() , (50)
, (50)
![]() , (51)
, (51)
![]() ,
, ![]() . (52)
. (52)
В соотношениях (42) - (52) введены следующие обозначения: В с соответствующими нижними индексами - биомасса основных и вторичных побегов, биомасса корней макрофитов, клубеньков и вновь образованных клубеньков ![]() ; верхний индекс "p" обозначает, что данная переменная относится к предыдущему дню; Ph - валовая скорость фотосинтеза основных побегов макрофитов
; верхний индекс "p" обозначает, что данная переменная относится к предыдущему дню; Ph - валовая скорость фотосинтеза основных побегов макрофитов ![]() ; R - скорость дыхания основных побегов макрофитов
; R - скорость дыхания основных побегов макрофитов ![]() ;
; ![]() - доля отмершей биомассы, которая принимает участие в процессе роста макрофитов
- доля отмершей биомассы, которая принимает участие в процессе роста макрофитов ![]() ;
; ![]() - клубеньковый поток, который используется для роста основных побегов макрофитов
- клубеньковый поток, который используется для роста основных побегов макрофитов ![]() ; множитель
; множитель ![]() характеризует воздействие световых условий на образование и развитие вторичных побегов;
характеризует воздействие световых условий на образование и развитие вторичных побегов; ![]() ,
, ![]() ,
, ![]() - доли основных и вторичных побегов, а также доля корневой биомассы, переносимые к вновь образуемым клубенькам;
- доли основных и вторичных побегов, а также доля корневой биомассы, переносимые к вновь образуемым клубенькам; ![]() и
и ![]() - соответственно скорости роста корней и новых клубеньков;
- соответственно скорости роста корней и новых клубеньков; ![]() - параметр, который принимается равным 0, если
- параметр, который принимается равным 0, если ![]() , и 1, если
, и 1, если ![]() , где
, где ![]() - Юлианская дата в момент начала образования новых клубеньков;
- Юлианская дата в момент начала образования новых клубеньков; ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() , таким образом, через семь дней развития 25% клубенькового потока направляется в корневую систему макрофитов.
, таким образом, через семь дней развития 25% клубенькового потока направляется в корневую систему макрофитов.
Из 29 эмпирических параметров данного модуля значения для 22-х из них были выбраны из литературы. Остальные оценивались в процессе калибровки модели. Принималось, что рост макрофитов начинался в озерах с того дня, когда сумма положительных температур достигала порядка 1500°С - 1700°С (в зависимости от конкретных особенностей той или иной озерной экосистемы). При описании процесса фотосинтеза использовалась кинетика Михаэлиса-Ментен, при этом учитывалось многофакторное его лимитирование световыми условиями и условиями биогенного питания, а также влияние температуры.
Модель экосистемы пелагиали озера Плещеево рассматривается в работе (Кучай, 1993). В данной работе разработан еще один вариант модели, который предполагает минимальную структуру модели и основан на максимально возможном использовании специфики озера и эмпирических связей, полученные при обработке данных гидробиологических экспедиций. Озеро Плещеево имеет ярко выраженную литораль - полосу прибрежного мелководья. Эта часть водоема может рассматриваться как самостоятельный природный комплекс. Следует отметить, что при всей важности литоральной зоны как барьера пелагиали относительно водосбора ее площадь составляет 20% от акватории озера, а объем - 2% от водной массы озера. Кроме того, по данным лимнологических исследований, ведущая роль в продукционном процессе в озере принадлежит фитопланктону пелагиальной зоны, на долю которого приходится 84% вновь синтезированного органического вещества. Вклад высшей водной растительности составляет третью часть продукции литоральной зоны (то есть около 3% общей продукции, создаваемой автотрофами). На этом основании в настоящем варианте модели экосистема озера представлена его глубоководной пелагиальной зоной (максимальная глубина озера 26 метров).
Число слоев в описываемом варианте равно двум., так как функционирование пелагиали озера тесно связано с его термическим режимом, при котором происходит вертикальное расслоение водной толщи (образование эпилимниона и гиполимниона с формированием в последнем анаэробных условий). Взаимодействие этих зон на протяжении вегетационного периода в значительной степени определяет динамику компонентов экосистемы. В связи с этим объем пелагиали разделяется на две характерные зоны - фотическую, простирающуюся от поверхности озера до глубины 12 метров, и гиполимнион - от глубины 12 метров до дна.
В модели используются следующие агрегированные переменные:
A - фитопланктон (![]() );
);
Z - зоопланктон (![]() );
);
R - рыбы;
PP - неорганический растворенный фосфор в зоне фотосинтеза (![]() );
);
NP - неорганический растворенный азот в зоне фотосинтеза (![]() );
);
PH - неорганический растворенный фосфор в гиполимнионе (![]() );
);
NH - неорганический растворенный азот в гиполимнионе (![]() );
);
DP - детрит в эпилимнионе (![]() );
);
DH - детрит в гиполимнионе (![]() ).
).
По характеру микрофлоры (то есть редуцентов и, следовательно, по характерным продуктам распада органического вещества в седиментах) озеро Плещеево относится к типу озер, где при наличии значительного содержания сульфатов идут процессы их редукции с образованием сероводорода. Процесс сульфат-редукции теснейшим образом связан с циклом фосфора. Поэтому в модели оценивается содержание сероводорода в гиполимнионе, что позволяет в какой-то степени характеризовать анаэробность гиполимниона при условии, что кислород не включен в число фазовых переменных.
В модели формализованы:
·продукционные процессы - фотосинтез за счет энергии солнечной радиации PRA, прирост биомассы зоопланктона JNZ и рыб JNR за счет выедания ими соответственно фитопланктона и зоопланктона;
·траты в процессе жизнедеятельности фитопланктона LSA, зоопланктона LSZи рыб LSR;
·деструкция органического вещества отмерших организмов - восстановление минеральных форм азота и фосфора согласно стехиометрическому соотношению C:N:P = 106:16:1, характерному для фитопланктона в среднем;
·физические процессы взаимодействия зон пелагиали.
Все эти процессы зависят от климатических факторов: солнечной радиации J и температуры воды T. Параметры модели с указанием их экологического смысла и их численные значения, которые были использованы при проведении расчетов, представлены в таблице 1.
Таблица 1. Отдельные параметры модели.
| Обозначение | Определение | Величина | Единица измерения |
| Ach_Max | Максимальное ассимиляционное число | 0,4 | |
| kChl | Константа относительного содержания хлорофилла в биомассе фитопланктона | 0,05 - 0,1 | |
| Константа полунасыщения по азоту в функции роста фитопланктона | 0,15 | - | |
| Константа полунасыщения по фосфору в функции роста фитопланктона | 0,02 | - | |
| kJNZA | Максимальная скорость выедания фитопланктона зоопланктоном | 0,7 | d-1 |
| kJNZD | Максимальная скорость выедания детрита зоопланктоном | 0,4 | d-1 |
| kA | Показатель степени величины биомассы и функции роста фитопланктона | 0,33 | - |
| kTA | Константа температурной функции | 0,09 | - |
| k1 | Константа FJ | 0,35 | - |
| k2 | 0,009 | - | |
| k3 | 2,39 | - | |
| k4 | 0,38 | - | |
| k5 | 7,24 | - | |
| k6 | 0,46 | - | |
| R | Альбедо | 0,07 | - |
| kMBA | Константа скорости метаболических выделений фитопланктона | 0,2 | - |
| kMRA | Скорость естественной смертности фитопланктона | 0,1 | d-1 |
| ANC | Отношение N:Cв клетках фитопланктона | 0,176 | - |
| APC | Отношение P:Cв клетках фитопланктона | 0,024 | - |
| kJNZ | Скорость роста зоопланктона при 0°С | 0,18 | d-1 |
| kLZ | Константа функции потерь зоопланктона | 0,35 | - |
| kMRZ | Константа функции смертности зоопланктона | 2,0 | - |
| TJNZ | Константа температурной функции | 0,09 | - |
| kZ | Константа функции роста зоопланктона | 2,0 | |
| TLZ | Константа температурной функции потерь зоопланктона | 0,08 | - |
| kAS | Коэффициент ассимиляции пищи зоопланктоном | 0,65 | - |
| kL | Скорость разложения детрита лабильной фракции в аэробных условиях | 2,4?10-3 | d-1 |
| kLH | Скорость разложения детрита лабильной фракции в анаэробных условиях | 0,058 | d-1 |
| kS | Скорость разложения детрита стойкой фракции в аэробных условиях | 0,007 | d-1 |
| kSH | Скорость разложения детрита стойкой фракции в анаэробных условиях | 0,006 | d-1 |
| kVD | Скорость оседания детрита | ||
| VE | Объем эпилимниона | 425,276?106 | m3 |
| VH | Объем гиполимниона | 146,224?106 | m3 |
| SH | Площадь сечения, разделяющего эпилимнион и гиполимнион | 25,5?106 | m2 |
| S0, S1, S2 | Константы функции |
48,02; -1,694; -0,017 | - |
| V0, V1, V2 | Константы функции |
585,408; -48,565; 0,99 | - |
Модель представлена системой дифференциальных уравнений.
Уровень I - дифференциальные уравнения:
![]() ; (1)
; (1)
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() ; (4)
; (4)
![]() ; (5)
; (5)
![]() ; (6)
; (6)
![]() ; (7)
; (7)
![]() ; (8)
; (8)
![]() . (9)
. (9)
Уровень II - скорости процессов:
![]() ; (10)
; (10)
![]() ; (11)
; (11)
![]() ; (12)
; (12)
![]() ; (13)
; (13)
![]() ; (14)
; (14)
![]() ; (15)
; (15)
![]() ; (16)
; (16)
![]() ; (17)
; (17)
![]() ; (18)
; (18)
![]() ; (19)
; (19)
![]() ; (20)
; (20)
![]() ; (21)
; (21)
![]() . (22)
. (22)
Уровень III - лимитирующие факторы и вспомогательные уравнения:
![]() ; (23)
; (23)
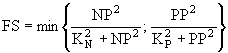 ; (24)
; (24)
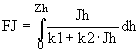 ,
, ![]() ; (25)
; (25)
![]() ,
, ![]() ; (26)
; (26)
![]() ; (27)
; (27)
![]() ,
, ![]() ; (28)
; (28)
![]() ; (29)
; (29)
![]() ; (30)
; (30)
![]() ; (31)
; (31)
![]() ; (32)
; (32)
![]() . (33)
. (33)
В модели предполагается, что скорости процессов фотосинтеза, роста биомассы фитопланктона и потребление ими биогенных элементов пропорциональны и химический состав клеток фитопланктона постоянен. Продукция фитопланктона PRA представлена средним по глубине значением фотосинтеза в эвфотической зоне озера глубиной Zh:
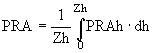 , (34)
, (34)
где PRAh - фотосинтез на горизонте h, величина которого в модели оценивается через максимальный по глубине фотосинтез Р и функциональную поправку ![]() , отражающую изменение фотосинтеза в зависимости от освещенности на глубине h:
, отражающую изменение фотосинтеза в зависимости от освещенности на глубине h: ![]() . Поскольку в настоящей модели не учитывается деление фитопланктона на группы, то целесообразно оценить
. Поскольку в настоящей модели не учитывается деление фитопланктона на группы, то целесообразно оценить ![]() , характеризующую сообщество водорослей в целом. Анализ данных по зависимости между проникающей в воду радиацией и фотосинтезом фитопланктона волжских водохранилищ показал, что если не учитывать явление фотоингибирования, то эту зависимость можно описать следующим соотношением (Пырина, 1979):
, характеризующую сообщество водорослей в целом. Анализ данных по зависимости между проникающей в воду радиацией и фотосинтезом фитопланктона волжских водохранилищ показал, что если не учитывать явление фотоингибирования, то эту зависимость можно описать следующим соотношением (Пырина, 1979):
![]() . (35)
. (35)
Здесь ![]() ,
, ![]() - энергия падающей радиации.
- энергия падающей радиации.
Предполагается, что в озере Плещеево зона максимального по глубине фотосинтеза - двухметровая поверхностная зона. Так как в условиях светового насыщения интенсивность фотосинтеза определяется скоростью ферментативных (темновых) реакций и зависит только от температуры воды, то
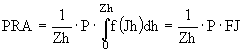 . (36)
. (36)
Известно, что фотосинтез через ассимиляционное число Ach связан с концентрацией хлорофилла "а" Chlв воде: ![]() . Ассимиляционное число сильно меняется в зависимости от условий среды (температуры воды, содержания в ней биогенных элементов) и биомассы фитопланктона А, с которой оно связано обратно пропорциональной зависимостью (Страшкраба, Гнаук, 1989). В модели принято, что
. Ассимиляционное число сильно меняется в зависимости от условий среды (температуры воды, содержания в ней биогенных элементов) и биомассы фитопланктона А, с которой оно связано обратно пропорциональной зависимостью (Страшкраба, Гнаук, 1989). В модели принято, что ![]() , где
, где ![]() - максимальное ассимиляционное число, характеризующее оптимальные условия среды при минимальной биомассе фитопланктона, а функции FT, FAи FS - соответствующие поправки при отклонениях от таковых. Обобщенная функция для определения интенсивности фотосинтеза имеет следующий вид:
- максимальное ассимиляционное число, характеризующее оптимальные условия среды при минимальной биомассе фитопланктона, а функции FT, FAи FS - соответствующие поправки при отклонениях от таковых. Обобщенная функция для определения интенсивности фотосинтеза имеет следующий вид:
![]() . (37)
. (37)
Формализация продукции зоопланктона в модели основана на предположениях о том, что источником питания для зоопланктона служат фитопланктон и детрит, суммарная концентрация которых рассматривается как "обобщенная" пища. Интенсивность роста зависит от температуры воды. Проблема избирательности питания не рассматривается. Аналогичным образом описана в модели продукция рыб. Потери биомассы в процессе развития зоопланктона и рыб (метаболические выделения и естественная смертность) представлены в модели функциями температуры и биомассы.
Процессы распада органического вещества формализованы традиционным образом: скорость распада RDпредполагается пропорциональной количеству органического вещества с температурной поправкой Вант-Гоффа. Регенерация органического азота и фосфора сбалансирована в соответствии со стехиометрическим соотношением.
При деструкции органического вещества в гиполимнионе происходит образование сероводорода ![]() , так как из белка клеток отмершего фитопланктона освобождается сера S. В модели полагается, что отношение P:S в фитопланктоне равно 1. Для определения соотношения между отдельными элементами в исходном планктоне и количеством восстановленной серы сульфатов используется эмпирическое соотношение (в атомах):
, так как из белка клеток отмершего фитопланктона освобождается сера S. В модели полагается, что отношение P:S в фитопланктоне равно 1. Для определения соотношения между отдельными элементами в исходном планктоне и количеством восстановленной серы сульфатов используется эмпирическое соотношение (в атомах): ![]() . Эта формула устанавливает связь между органическим углеродом и расходуемой сульфатной серой на полное окисление органического вещества планктона (освобождение серы из белков связано с полной минерализацией органического веществ). Таким образом, по количеству органического вещества, подвергающемуся деструкции в гиполимнионе, оценивается содержание в воде сероводорода.
. Эта формула устанавливает связь между органическим углеродом и расходуемой сульфатной серой на полное окисление органического вещества планктона (освобождение серы из белков связано с полной минерализацией органического веществ). Таким образом, по количеству органического вещества, подвергающемуся деструкции в гиполимнионе, оценивается содержание в воде сероводорода.
В имитационной модели экосистемы озерного рыбопитомника (Казанский, Михайлов, 1989) исследуются особенности сезонной динамики основных биотических компонент экосистемы озера, концентрации биогенных элементов - азота и фосфора, детрита, растворенного в воде кислорода. Компонентами модели являются: 1) фитопланктон; 2) хищный зоопланктон; 3) мирный зоопланктон; 4) зообентос; 5) бактериопланктон; 6) рыбы; 7) детрит в водной толще; 8) мертвое органическое вещество ила. Из-за отсутствия данных о процессах в илах и динамике РОВ сделаны ряд упрощений. РОВ условно включено в состав детрита и рассматривается с ним совместно. Процессы бактериального и биохимического разложения ОВ донных отложений, сорбция биогенных элементов иловыми частицами и их диффузия из порового раствора в придонные слои воды сведены к результирующему показателю обобщенной деструкции органики илов. В экосистеме выделены верхняя область водной массы, где продуцирует фитопланктон, и нижняя область, включающая придонные слои воды, активный слой ила и зообентос.
Циклы биогенных элементов замыкаются в результате разложения детрита в водной массе и минерализации органического вещества илов. Выход биогенов из оборота происходит за счет захоронения органики в ДО, вылета хирономид и вылова рыбы. Внешние поступления складываются из управляемого потока (вносимых удобрений) и неуправляемого потока (аллохтонной органики водных притоков и осадков). Как показал предварительный анализ, состояние экосистемы регулируется биогенами, кислородным режимом, интенсивностью солнечной радиации, температурой воды.
В работе (Булдовская, Даценко, 1994) рассматривается математическая модель развития фитопланктона в хорошо перемешиваемых водах водохранилищ. Объект моделирования - Учинское водохранилище. Гидрологический блок модели максимально упрощен. Предполагается, что приемлемо использование точечной модели с описанием водообмена согласно гипотезе идеального перемешивания. Поэтому динамика модельных переменных задается в модели уравнением следующего вида:
![]() , (1)
, (1)
где С - концентрация веществ в водоеме ![]() ;
; ![]() - концентрация веществ в притоке
- концентрация веществ в притоке ![]() ; q - приток воды в водохранилище
; q - приток воды в водохранилище ![]() ; V - объем водоема
; V - объем водоема ![]() ;
; ![]() - шаг по времени (с).
- шаг по времени (с).
Концептуальная схема модели.
Фитопланктон разделен в модели на две группы по систематическому признаку. Необходимость разделения фитопланктона на группы вызвана особенностями Учинского водохранилища, в котором периоды активизации диатомовых и синезеленых резко отделены друг от друга, а между ними фитопланктон в водохранилище практически отсутствует. В данной работе детрит не рассматривался как выходная переменная модели, поскольку наблюдений за изменением его концентрации в водохранилище в моделируемый промежуток времени не проводилось, однако введение в модель этой переменной позволило точнее учесть скорости трансформации вещества в водоеме.
При описании потоков вещества приняты следующие обозначения: ![]() - поток от переменной X к переменной Y;
- поток от переменной X к переменной Y; ![]() - поток к переменной Xиз внешних источников рассматриваемой системы;
- поток к переменной Xиз внешних источников рассматриваемой системы; ![]() - поток от переменной Xиз рассматриваемой системы; DA, BG - концентрации
- поток от переменной Xиз рассматриваемой системы; DA, BG - концентрации ![]() соответственно диатомовых и синезеленых водорослей; N, P- концентрации
соответственно диатомовых и синезеленых водорослей; N, P- концентрации ![]() минерального азота и фосфора соответственно; D - концентрация детрита
минерального азота и фосфора соответственно; D - концентрация детрита ![]() .
.
Модель может быть представлена в виде следующей системы уравнений:
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() , (4)
, (4)
![]() , (5)
, (5)
![]() . (6)
. (6)
Модель описывает следующие процессы:
Потребление фосфора ![]() ,
, ![]() и азота
и азота ![]() ,
, ![]() диатомовыми и синезелеными водорослями.
диатомовыми и синезелеными водорослями.
Оно описывается следующей формулой:
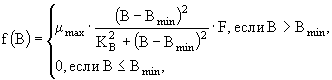 (7)
(7)
где ![]() - максимальная скорость потребления биогенного элемента
- максимальная скорость потребления биогенного элемента ![]() ; B - концентрация биогенного элемента в воде
; B - концентрация биогенного элемента в воде ![]() ;
; ![]() - его минимальная концентрация в воде, при которой он не потребляется
- его минимальная концентрация в воде, при которой он не потребляется ![]() ;
; ![]() - константа полунасыщения
- константа полунасыщения ![]() ; F - концентрация фитопланктона в воде
; F - концентрация фитопланктона в воде ![]() .
.
В модели учитывается влияние на процесс потребления биогенных веществ различных факторов: освещенности и температуры воды. Совместным влиянием факторов определяется поток ![]() , где
, где ![]() - функция, с помощью которой определяется световое лимитирование фитопланктона в слое
- функция, с помощью которой определяется световое лимитирование фитопланктона в слое ![]() с учетом фотоингибирования и самозатенения фитопланктона,
с учетом фотоингибирования и самозатенения фитопланктона, ![]() - функция, с помощью которой учитывается влияние температуры воды. Эти функции заданы в модели следующим образом (Страшкраба, Гнаук, 1989):
- функция, с помощью которой учитывается влияние температуры воды. Эти функции заданы в модели следующим образом (Страшкраба, Гнаук, 1989):
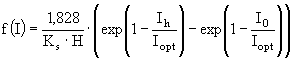 , (8)
, (8)
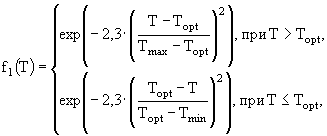 (9)
(9)
где ![]() ;
; ![]() - освещенность на поверхности;
- освещенность на поверхности; ![]() - оптимальная освещенность для фитопланктона данной группы
- оптимальная освещенность для фитопланктона данной группы ![]() ; Н - глубина фотического слоя (м);
; Н - глубина фотического слоя (м); ![]() - коэффициент ослабления света,
- коэффициент ослабления света, ![]() ;
; ![]() - коэффициент ослабления света водой
- коэффициент ослабления света водой ![]() ,
, ![]() - коэффициент ослабления света фитопланктоном
- коэффициент ослабления света фитопланктоном ![]() ; T - температура воды (°С);
; T - температура воды (°С); ![]() ,
, ![]() ,
, ![]() - значения температуры воды, определяющие соответственно оптимальные и граничные условия развития выделенных групп фитопланктона (°С).
- значения температуры воды, определяющие соответственно оптимальные и граничные условия развития выделенных групп фитопланктона (°С).
Рост водорослей G.
Он рассматривается в модели как следствие включения в состав живых клеток потребленных биогенных элементов и увеличения биомассы за счет других компонент, составляющих вещество фитопланктона: углерода, водорода, кремния, серы и др. В данной модели рост описывается для каждой группы водорослей тремя потоками:
![]() . (10)
. (10)
Количественно эти потоки связаны соотношением стехиометрических коэффициентов ![]() , где
, где ![]() и
и ![]() - стехиометрические коэффициенты для фосфора и азота соответственно, а
- стехиометрические коэффициенты для фосфора и азота соответственно, а ![]() - суммарный стехиометрический коэффициент для всех других веществ, включаемых в биомассу фитопланктона. Из этого соотношения видно, что рост водорослей определяется в основном потоком
- суммарный стехиометрический коэффициент для всех других веществ, включаемых в биомассу фитопланктона. Из этого соотношения видно, что рост водорослей определяется в основном потоком ![]() , который задается пропорционально потреблению лимитирующего элемента. Для диатомовых можно считать, что
, который задается пропорционально потреблению лимитирующего элемента. Для диатомовых можно считать, что
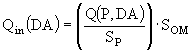 , (11)
, (11)
так как в период их развития азота в водоеме достаточно много. В августе же во время "цветения" синезеленых водорослей в Учинском водохранилище наблюдаются минимальные концентрации азота при довольно высоком содержании фосфора. Поэтому предполагается, что фосфорное лимитирование развития водорослей может сменяться азотным (Михеева, 1983). Данное предположение в модели отражено уравнением
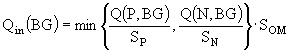 . (12)
. (12)
Отмирание фитопланктона.
Оно описывается в модели потоками ![]() и
и ![]() , где
, где ![]() ,
, ![]() ,
, ![]() - коэффициент смертности фитопланктона, который зависит от температуры воды. Для его параметризации используются следующие зависимости:
- коэффициент смертности фитопланктона, который зависит от температуры воды. Для его параметризации используются следующие зависимости:
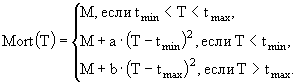 (13)
(13)
Здесь M - коэффициент смертности в интервале оптимальных температур роста фитопланктона ![]() ; a и b - коэффициенты крутизны кривой увеличения смертности при
; a и b - коэффициенты крутизны кривой увеличения смертности при ![]() и
и ![]() . Предполагается, что на убыль диатомовых в фазе спада их развития большое влияние оказывает зоопланктон, так как в конце мая в водохранилище наблюдается интенсивное его развитие. Для учета этого факта в модель для данного периода вводится добавка к коэффициенту смертности.
. Предполагается, что на убыль диатомовых в фазе спада их развития большое влияние оказывает зоопланктон, так как в конце мая в водохранилище наблюдается интенсивное его развитие. Для учета этого факта в модель для данного периода вводится добавка к коэффициенту смертности.
Разложение детрита.
Оно описывается уравнением реакции первого порядка, константа которой зависит от температуры воды. При этом регенерация биогенов задается пропорционально их стехиометрическим коэффициентам. Поток ![]() определяет выведение части детритного вещества, не содержащего N и P, из системы рассматриваемых в модели элементов. Константы скоростей в уравнениях, описывающих этот блок модели
определяет выведение части детритного вещества, не содержащего N и P, из системы рассматриваемых в модели элементов. Константы скоростей в уравнениях, описывающих этот блок модели ![]() и
и ![]() , представляют собой скорости перехода детритных форм в минеральные.
, представляют собой скорости перехода детритных форм в минеральные.
Значения основных параметров модели.
| Параметр | Диатомовые | С/зеленые | Параметр | Диатомовые | С/зеленые |
| 0,05 | 0,06 | 1,0 | 1,0 | ||
| 0,009 | 0,003 | - | 12,0 | ||
| 0,60 | 0,30 | 140,0 | 130,0 | ||
| 0,03 | 0,02 | 0,015 | 0,0015 | ||
| 3,0 | 17,0 | 8,5 | 20,0 | ||
| 8,7 | 23,0 | 9,5 | 27,0 | ||
| 11,0 | 33,0 | a | 0,0003 | 0,004 | |
| Н | 4,0 | 4,0 | b | 0,009 | 0,009 |
| 3000,0 | 5500,0 | 0,005 | 0,005 | ||
| 0,02 | 0,02 | 0,001 | 0,001 | ||
| 0,01 | 0,01 |
Оценка чувствительности модели к значениям параметров показала, что наибольшее влияние на модельные результаты концентраций фитопланктона оказывают параметры, определяющие лимитирование роста биогенными элементами, и параметры отмирания. При этом для диатомовых более важны значения ![]() ,
, ![]() и М, а для моделирования развития синезеленых - a, Mи
и М, а для моделирования развития синезеленых - a, Mи ![]() . На величины моделируемых концентраций биогенных веществ наибольшее влияние оказывают параметры, определяющие скорости их потребления фитопланктоном.
. На величины моделируемых концентраций биогенных веществ наибольшее влияние оказывают параметры, определяющие скорости их потребления фитопланктоном.
Данная модель использовалась в качестве предварительной основы для более детального исследования динамики круговорота соединений фосфора в Учинском водохранилище по модели фосфорной системы (Булдовская, Леонов, 1996):
![]() , (14)
, (14)
где ![]() - концентрации соответствующего компонента фосфорной системы,
- концентрации соответствующего компонента фосфорной системы, ![]() - суммарная скорость его биохимических превращений,
- суммарная скорость его биохимических превращений, ![]() - суммарная скорость внешних потоков (адвективный внос и вынос, обмен между водой и дном).
- суммарная скорость внешних потоков (адвективный внос и вынос, обмен между водой и дном).
В модели предусмотрен аппарат ее настройки на условия конкретного водоема - особая структура уравнений модели. Уравнения, описывающие удельные скорости основных процессов жизнедеятельности фитопланктона (потребление субстратов питания (UPF), метаболических выделений (LPF), отмирания (SPF)), имеют следующий вид:
![]() , (15)
, (15)
где ![]() - максимальная скорость потребления субстрата, RTFи RIF - функции, учитывающие зависимость скорости от температурных и световых условий, RNP - функция коррекции максимальной скорости потребления субстрата на отношение минерального азота и фосфора в воде (
- максимальная скорость потребления субстрата, RTFи RIF - функции, учитывающие зависимость скорости от температурных и световых условий, RNP - функция коррекции максимальной скорости потребления субстрата на отношение минерального азота и фосфора в воде (![]() ), FP - биомасса фитопланктона в единицах фосфора, DIP - концентрация растворенного неорганического фосфора. Скорость метаболических выделений фитопланктона в общем виде задается следующим уравнением:
), FP - биомасса фитопланктона в единицах фосфора, DIP - концентрация растворенного неорганического фосфора. Скорость метаболических выделений фитопланктона в общем виде задается следующим уравнением:
![]() , (16)
, (16)
а скорость отмирания - уравнением
![]() . (17)
. (17)
В соотношениях (16), (17) ![]() ,
, ![]() ,
, ![]() и
и ![]() - эмпирические константы.
- эмпирические константы.
Расчеты с помощью модели для Учинского водохранилища выполнялись в основном с набором коэффициентов, который был ранее определен при исследовании процессов трансформации фосфора в других водоемах с использованием результатов достаточно детальных наблюдений за изменчивостью характеристик водной среды и концентрацией форм фосфора в них. Некоторая корректировка коэффициентов модели связана с существенными различиями групп фитопланктона, доминирующими в различные сезоны. По этой же причине моделирование для периода с июня по сентябрь месяцы, когда в фитопланктоне доминируют синезеленые водоросли, проводилось с одним набором коэффициентов, а в остальную часть года, когда доминируют диатомовые - с другим.
В работе (Якушев, Михайловский, 1993) рассматривается математическая модель химико-биологических циклов фосфора, азота и кислорода и их сезонной изменчивости в Белом море. Моделирование биогеохимических циклов является важным элементом комплексного экологического исследования океанских и морских вод. Задача создания таких моделей становится все более актуальной, так как воздействия на экосистему вызывают прежде всего изменения интенсивности потоков соединений химических элементов, что приводит к нарушениям в функционировании биоты. Кроме того, все более очевидной становится задача исследования всех деталей глобального цикла углерода, определяющего изменение климата Земли, и важного элемента этого цикла - круговорота соединений углерода в океане.
Каждый глобальный биогеохимический цикл состоит из множества локальных круговоротов соответствующего биогенного элемента различного масштаба. При этом, если глобальный цикл, как правило, полностью замкнут, то локальные круговороты существенно незамкнуты. Следует также отметить, что степень их незамкнутости обычно возрастает с уменьшением масштаба круговорота. Поэтому на уровне экосистемы такая незамкнутость весьма существенна и требует учета притока и оттока в рассматриваемую систему соответствующего биогенного элемента. Подобная структура глобальных биогеохимических циклов обусловливает их лабильность и, одновременно, устойчивость.
Выбор количества блоков в моделях морских (да и не только морских) экосистем теоретически связан с целью оптимального описания функционирования экосистемы. В существующих морских экологических моделях в качестве лимитирующего субстрата используется абстрактный "биогенный элемент", фосфор или, чаще всего, - азот. Последнее обстоятельство представляется с точки зрения гидрохимии несколько странным, так как биогеохимический цикл фосфора проще биогеохимического цикла азота, и, кроме того, для азота существует ряд нерешенных вопросов, связанных с процессами денитрификации и азотфиксации. В то же время вопрос о том, какой же элемент "более" лимитирует, по-видимому, не имеет смысла, так как существуют свидетельства о преимущественном лимитировании как одним, так и другим элементом в различных регионах и в разное время года. Рассматривая трансформацию только одного биогенного элемента, все существующие модельные схемы так или иначе базируются на факте безусловного выполнения стехиометрических соотношений, что в целом не верно. Вопрос о включении в модель параллельно циклов нескольких биогенных элементов остается открытым. Это и является теоретической целью данной работы. В основу предлагаемой работы заложено совместное описание циклов двух биогенных элементов - азота и фосфора. Прикладная цель данной работы - описать качественные черты сезонной изменчивости химико-биологических циклов азота, фосфора и кислорода на примере открытых вод Белого моря и откалибровать данную модель, чтобы ее можно было использовать в качестве модельного блока, вместе с моделью течений при имитационном моделировании развития экологической ситуации в Белом море.
Так как цель модели - отразить основные черты химико-биологических циклов, то из живых организмов модель рассматривает только фито- и зоопланктон, биомасса которых (от 10 - 500 мг/м3 летом до нескольких г/м3 весной) значительно превышает биомассу инфузорий и бактерий (2 - 30 мг/м3), в то же время биогеохимическая роль бактерий отражена при окислении ОВ. Было принято, что стехиометрические отношения безусловно выполняются в живых организмах, а нарушение стехиометрии начинается при окислении ОВ, поэтому процессы окисления фосфора и азота описаны независимо. Нелинейные члены присутствуют лишь при описании питания организмов. В модели рассматриваются концентрации фитопланктона ![]() , зоопланктона
, зоопланктона ![]() , форм фосфора: фосфатов
, форм фосфора: фосфатов ![]() , взвешенного органического фосфора
, взвешенного органического фосфора ![]() , растворенного органического фосфора
, растворенного органического фосфора ![]() , форм азота: нитратов
, форм азота: нитратов ![]() , нитритов
, нитритов ![]() , аммонийного азота
, аммонийного азота ![]() , взвешенного органического азота
, взвешенного органического азота ![]() , растворенного органического азота
, растворенного органического азота ![]() и растворенного кислорода
и растворенного кислорода ![]() (всего 11 переменных).
(всего 11 переменных).
Таблица 1. Параметры модели.
| Обозначение | Определение | Величина | Единица измерения |
| Максимальная удельная скорость роста фитопланктона | 5,5 | сут-1 | |
| Константа полунасыщения по фосфатам | 0,25 | мкг-ат/л | |
| Пороговая концентрация фитопланктона | 1,6 | мг/м3 | |
| Удельная скорость дыхания фитопланктона | 0,15 | сут-1 | |
| Удельная скорость отмирания фитопланктона | 0,05 | сут-1 | |
| Удельная скорость экскреции фитопланктона | 0,15 | сут-1 | |
| Максимальная скорость потребления фитопланктона зоопланктоном | 0,9 | сут-1 | |
| Константа полунасыщения по фитопланктону | 5,0 | б/р | |
| Удельная скорость дыхания зоопланктона | 0,10 | сут-1 | |
| Удельная скорость отмирания зоопланктона | 0,05 | сут-1 | |
| Максимальная скорость потребления ВОВ зоопланктоном | 0,2 | сут-1 | |
| Константа полунасыщения по ВОВ | 0,5 | б/р | |
| Пороговая концентрация ВОВ | 0,0001 | мкг-ат/л | |
| Удельная скорость автолиза ВОВ | 0,13 | сут-1 | |
| Усвояемость пищи зоопланктоном | 0,7 | б/р | |
| Соотношение жидких и твердых экскретов зоопланктона | 0,4 | б/р | |
| Коэффициент фосфатофикации ВОВ и РОВ соответственно | 0,002; 0,010 | сут-1 | |
| Коэффициент формулы Фашама | 1,50 | б/р | |
| Константа полунасыщения по нитратам и аммонию соответственно | 0,3; 0,3 | мкг-ат/л | |
| Удельная скорость аммонификации РОВ и ВОВ соответственно | 0,08; 0,05 | сут-1 | |
| Удельная скорость первой и второй стадии нитрификации соответственно | 0,09; 0,04 | сут-1 | |
| Удельная скорость погружения фитопланктона, зоопланктона и детрита соответственно | 1,8; 0,1; 2,0 | м/сут | |
| Коэффициенты обмена с нижележащими водами для лета и зимы соответственно | 0,001; 0,007 | сут-1 | |
| Содержание азота и фосфора на единицу биомассы | 0,014; 0,001 | мкг-ат/л | |
| Содержание кислорода на единицу биомассы | 0,005 | мл/мг |
Уравнения модели:
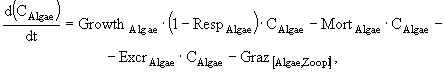 (1)
(1)
![]() (2)
(2)
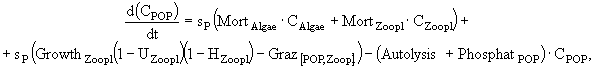 (3)
(3)
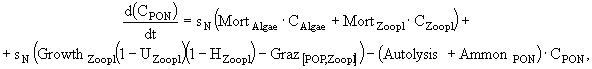 (4)
(4)
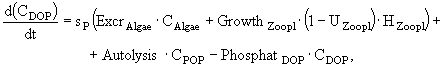 (5)
(5)
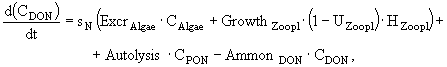 (6)
(6)
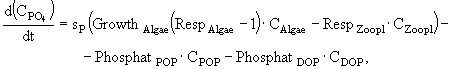 (7)
(7)
 (8)
(8)
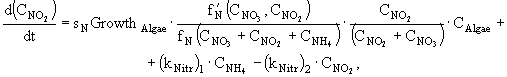 (9)
(9)
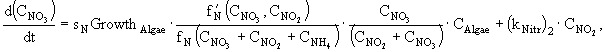 (10)
(10)
![]() (11)
(11)
Скорость роста фитопланктона ![]() задавалась в соответствии с формулами, учитывающими зависимость максимальной удельной скорости роста
задавалась в соответствии с формулами, учитывающими зависимость максимальной удельной скорости роста ![]() от температуры воды, условий освещенности и наличия биогенных элементов:
от температуры воды, условий освещенности и наличия биогенных элементов:
![]() , (12)
, (12)
![]() , (13)
, (13)
![]() . (14)
. (14)
В формуле (14) введены следующие обозначения: ![]() - оптимальная освещенность,
- оптимальная освещенность, ![]() - освещенность на горизонте Z,
- освещенность на горизонте Z, ![]() - освещенность на поверхности воды, которая зависит от времени,
- освещенность на поверхности воды, которая зависит от времени, ![]() - коэффициент экстинкции. Зависимость скорости роста фитопланктона от концентрации соединений азота и фосфора задается множителем
- коэффициент экстинкции. Зависимость скорости роста фитопланктона от концентрации соединений азота и фосфора задается множителем ![]() , где
, где 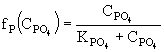 . Избирательность потребления соединений азота была описана в соответствии с формулой Фашама (Fashametal., 1990):
. Избирательность потребления соединений азота была описана в соответствии с формулой Фашама (Fashametal., 1990):
 (15)
(15)
Скорость роста зоопланктона ![]() складывается из потребления фитопланктона
складывается из потребления фитопланктона ![]() и взвешенного органического вещества
и взвешенного органического вещества ![]() :
:
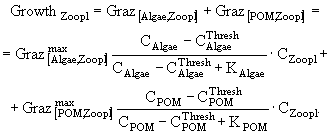 (16)
(16)
Значения коэффициентов модели выбирались по литературным данным, а также подбирались опытным путем. Их величины приведены в таблице.
Первые численные эксперименты с предложенной модельной схемой были посвящены описанию общих тенденций сезонной изменчивости рассматриваемых параметров для средних условий пелагиали Белого моря. Было решено рассматривать средневзвешенные концентрации компонентов для слоя, где обитают фотосинтетические организмы и, соответственно, осуществляется фотосинтез. Этой слой конкретно в Белом море можно в первом приближении считать совпадающим с верхним перемешанным слоем (ВКС). Годовая изменчивость толщины ВКС, а также освещенности и температуры, были заданы в качестве внешних параметров. Глубина ВКС в Белом море чрезвычайно изменчива: она меняется от 3 - 5 м в мае до 50 - 60 м в ноябре, при этом выраженность пикноклина также резко уменьшается от весны к осени, а зимой он, видимо, фактически размывается. Это чрезвычайно важно для определения таких параметров модели, как удельная скорость фотосинтеза и скорость гравитационного оседания взвеси.
Расчеты проводились на основе балансового уравнения
![]() , (17)
, (17)
в котором ![]() соответствует выделенным переменным модели, первое слагаемое в правой части задается уравнениями (1) - (11),
соответствует выделенным переменным модели, первое слагаемое в правой части задается уравнениями (1) - (11), ![]() - скорость гравитационного оседания для взвешенных компонентов. Последний член описывает поступление в эвфотический слой фосфатов и нитратов, коэффициент
- скорость гравитационного оседания для взвешенных компонентов. Последний член описывает поступление в эвфотический слой фосфатов и нитратов, коэффициент ![]() равен нулю для всех прочих компонентов,
равен нулю для всех прочих компонентов, ![]() - концентрация фосфатов (нитратов) ниже слоя фотосинтеза. Коэффициент
- концентрация фосфатов (нитратов) ниже слоя фотосинтеза. Коэффициент ![]() также рассматривался в качестве внешнего параметра и менял свое значение зимой и летом.
также рассматривался в качестве внешнего параметра и менял свое значение зимой и летом.
В работе (Inkala etal., 1997) рассматривается математическая модель воздействий климатических изменений на биогенную нагрузку, температурный режим и биомассу фитопланктона Финского залива.
Структура модели:
·блок для расчета речного стока;
·блок для расчета транспорта биогенов с речным стоком;
·нестационарная модель для расчета вертикального и горизонтального распределения температуры воды (максимальное число слоев = 30).
Эта модель включает в себя уравнения движения и сохранения энергии. Параметризация турбулентного обмена - на основании к-e теории. В качестве входных переменных используются данные по температуре воздуха, скорости ветра, влажности, облачности;
·модель для расчета динамики фитопланктона. Этот блок использует трехмерную гидродинамическую модель с десятью вертикальными слоями. Значения температуры воды в различных слоях берутся из результатов расчета по температурной модели.
Моделирование было выполнено с различной глубиной прогноза (25, 50, 100 лет) при различных сценариях возможных климатических изменений температурного (увеличение температуры поверхностного слоя воды на 0,3 - 6,2 °С) и ветрового (увеличение повторяемости ветров со скоростями > 7 м/с) режимов, изменений речного стока, биогенной нагрузки. Было показано, что средняя концентрация фитопланктона увеличится незначительно, поскольку наиболее важным лимитирующим фактором является биологически доступные питательные вещества. Вместе с тем, внешняя нагрузка биологически доступных биогенов не претерпит существенных изменений, поскольку более чем на 90% она состоит из промышленных и муниципальных стоков и по своей химической структуре мало подходит для утилизации фитопланктонными организмами. Весенние вспышки фитопланктона будут наблюдаться примерно на одну-две недели раньше, чем это имеет место на сегодняшний момент времени. При этом средние концентрации фитопланктона возрастут примерно на 10% к 2020 году (глубина прогноза 25 лет) и на 20% к 2090 (глубина прогноза 100 лет). Временные количественные изменения развития фитопланктона связаны с более быстрым ростом водорослей из-за повышения температуры воды и, как следствие, более эффективным использованием биогенных веществ. Усиление ветра приведет к более интенсивному перемешиванию поверхностных слоев воды, уменьшению поверхностной температуры воды, заглублению термоклина примерно на 1-2 метра (при глубинах примерно 60 м) и переносу фитопланктона в более глубокие слои.
Таблица 1. Переменные модели.
| Обозначение | Определение | Единица измерения |
| Концентрация азота в составе детрита | mg m-3 | |
| Концентрация аммонийного азота | mg m-3 | |
| Концентрация нитратного азота | mg m-3 | |
| Концентрация азота в клетках водорослей | mg m-3 | |
| Концентрация фосфора в составе детрита | mg m-3 | |
| Концентрация фосфора фосфатов | mg m-3 | |
| Концентрация фосфора в клетках водорослей | mg m-3 | |
| Биомасса водорослей | mg m-3 | |
| Нагрузка за счет азота в составе детрита | kg d-1 | |
| Нагрузка за счет аммонийного азота | kg d-1 | |
| Нагрузка за счет нитратного азота | kg d-1 | |
| Нагрузка за счет фосфора в составе детрита | kg d-1 | |
| Нагрузка за счет фосфора фосфатов | kg d-1 | |
| t | Время | d |
| h | Глубина | m |
| I | Суммарная радиация | MJ m-2 d-1 |
| T | Температура воды в слое | °C |
| Оптимальная температура | °C |
| Обозначение | Определение | Величина | Единица измерения |
| Скорость разложения соединений азота в составе детрита | 0.018 | d-1 | |
| Скорость оседания соединений азота в составе детрита | 4.0 | cm d-1 | |
| Скорость нитрификации | 0.15 | d-1 | |
| Скорость денитрификации | 4.0 | cm d-1 | |
| Коэффициент предпочтения | 1.0 | - | |
| Скорость разложения соединений фосфора в составе детрита | 0.02 | d-1 | |
| Скорость оседания соединений фосфора в составе детрита | 4.0 | cm d-1 | |
| Максимальная скорость роста фитопланктона | 2.5 | d-1 | |
| Коэффициент полунасыщения при поглощении соединений фосфора фитопланктоном | 250.0 | mg l-1 | |
| Коэффициент полунасыщения при поглощении соединений азота фитопланктоном | 60.0 | mg l-1 | |
| Минимальное значение отношения содержания фосфора в клетках фитопланктона к биомассе фитопланктона | 0.003 | gP gC-1 | |
| Максимальное значение отношения содержания фосфора в клетках фитопланктона к биомассе фитопланктона | 0.044 | gP gC-1 | |
| Минимальное значение отношения содержания азота в клетках фитопланктона к биомассе фитопланктона | 0.05 | gN gC-1 | |
| Максимальное значение отношения содержания азота в клетках фитопланктона к биомассе фитопланктона | 0.335 | gN gC-1 | |
| Максимальная скорость поглощения соединений фосфора фитопланктоном | 0.243 | gP gC-1 d-1 | |
| Максимальная скорость поглощения соединений азота фитопланктоном | 0.04 | gN gC-1 d-1 | |
| Максимальная скорость смертности фитопланктона | 0.05 | d-1 | |
| Предельное значение для быстрой седиментации | 0.06 | - | |
| Fast_sed | Ускорение быстрой седиментации | 2.0 | - |
| Оптимальное значение для солнечной радиации | 10.0 | MJ m-2 |
Уравнения модели.
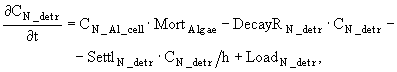 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
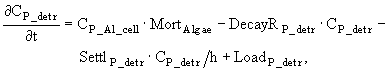 (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]()
![]() (7)
(7)
![]() (8)
(8)
Скорости процессов.
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
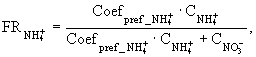 (13)
(13)
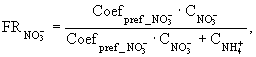 (14)
(14)
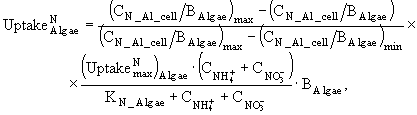 (15)
(15)
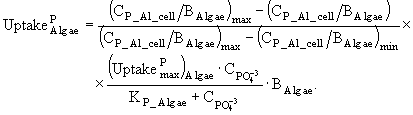 (16)
(16)
Лимитирующие факторы.
![]()
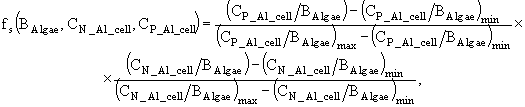 (17)
(17)
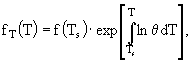 (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
Таблица 3. Константы для функции температурной коррекции.
| a (безразм.) | b (°C-1) | |
| 1.257 | -0.011 | |
| 1.020 | -0.001 |
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ