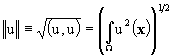Свойства дифференциальных операторов диффузионного и конвективного переноса
При разработке численной схемы принципиальным является положение о том, что решение дискретной задачи должно наследовать основные свойства дифференциальной задачи (Самарский, Вабищевич, 1999). Этого мы можем достичь, в частности, в том случае, когда сеточные операторы будут иметь те же основные свойства, что и дифференциальные операторы. Мы начнем с рассмотрения свойств дифференциальных операторов. Свойства сеточных операторов диффузионного и конвективного переноса будут рассмотрены ниже.
Для дальнейшего обсуждения нам потребуются некоторые важные понятия, определения и неравенства. Обозначим через 
(в дальнейшем просто Н) - гильбертово пространство со скалярным произведением 
для произвольных функций 
и 
, обращающихся в нуль на границе 
области решения 
, и нормой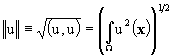 
. Если 
или 
, то оператор называется положительно полуопределенным (неотрицательным), причем равенство нулю скалярного произведения 
допускается на элементе 
, тождественно не равном нулю. Если равенство исключается, то есть 
при 
, то оператор 
называют положительным и пишут 
. Наконец, в случае более сильного неравенства 
, где 
- некоторая постоянная, общая для всех 
, оператор 
называют положительно определенным. Заметим, что если оператором 
является квадратная матрица, то для нее из условия положительности следует и положительная определенность. Введем, далее, в рассмотрение сопряженный оператор 
с помощью тождества Лагранжа 
. В том случае, когда 
и области определения операторов 
и 
совпадают, оператор 
называют самосопряженным. В этом случае из условия 
следует, что и 
. Норма оператора определяется обычным образом: 
. Принимая во внимание соотношение 
, получим 
. Оператор 
- симметричный и положительно полуопределенный.
Оператор диффузионного переноса, определяемый согласно (7), самосопряжен в Н на множестве функций, удовлетворяющих однородным граничным условиям: 
. Действительно, принимая во внимание формулу Грина, имеем
.
Отметим также, что рассматриваемый оператор диффузионного переноса при естественных ограничениях 
положительно определен. В случае граничных условий Дирихле для него верна оценка
, (12)
где Е - тождественный оператор, 
минимальное собственное значение оператора Лапласа. Оценка (12) следует из 
.
Рассмотрим теперь оператор конвективного переноса в различных формах (8) - (10). Принимая во внимание однородные граничные условия, имеем
.
Таким образом, установлена сопряженность с точностью до знака операторов конвективного переноса в дивергентной и недивергентной формах друг другу, то есть
. (13)
В силу последнего соотношения оператор конвективного переноса в симметричной форме (10) будет кососимметричным 
:
. (14)
При выполнении условия несжимаемости среды
(15)
кососимметричными будут и операторы конвективного переноса в недивергентном и дивергентном видах. Принципиальным при построении дискретных аппроксимаций конвективного переноса является то, что свойствокососимметричности для оператора 
имеет место при любых значениях скоростей 
, в том числе и не удовлетворяющих условию несжимаемости (15).
Полезны также оценки сверху для операторов конвективного переноса (Самарский, Вабищевич, 1999). Для операторов в формах (8), (9) имеем 
и поэтому
, (16)
где 
. В силу этого для операторов конвективного переноса, определяемых в соответствии с (8), (9), имеем
, (17)
где постоянная 
зависит только от дивергенции скорости и, в соответствии с (16), есть
. (18)
Приведем также оценки подчиненности оператора конвективного переноса оператору диффузионного переноса:
, (19)
с постоянной 
, зависящей от скорости. Для недивергентного оператора конвекции (8) имеем
то есть в неравенстве (19) при 
мы можем положить
. (20)
Аналогично, при 
получим
.
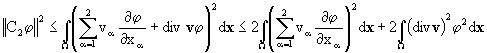Принимая во внимание неравенство Фридрихса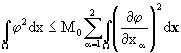 
, где постоянная 
, получим при 
оценку (19) с постоянной
. (21)
Аналогично для случая 
имеем 
, то есть
. (22)
Приведенные оценки (17), (19) служат ориентиром при исследовании дискретных аналогов операторов конвективного переноса. Естественно стремиться к тому, чтобы аналогичные свойства имели и разностные операторы диффузионного и конвективного переноса.
Суммируем установленные свойства операторов конвективного переноса в виде следующего утверждения (Самарский, Вабищевич, 1999).
Теорема 1. Операторы конвективного переноса обладают следующими свойствами:
·операторы конвективного переноса в недивергентной и дивергентной формах сопряжены с точностью до знака друг другу - равенство (13);
·оператор конвективного переноса в симметричной форме является кососимметричным - равенство (14);
·операторы конвективного переноса в недивергентной и дивергентной формах являются ограниченными - априорная оценка (17) и оценка (18);
·операторы конвективного переноса подчинены оператору диффузии - оценка (19) с постоянной 
, определяемой согласно соотношениям (20) - (22).
Приведем теперь некоторые простейшие априорные оценки для нестационарной задачи конвекции – диффузии (11) (Самарский, Вабищевич, 1999).
Теорема 2. Для задачи (11) при выполнении условий (12), (17), (19) имеют место следующие априорные оценки:
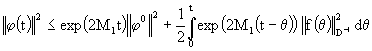, (23)
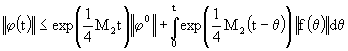, (24)
, (25)
где 
, 
.
Доказательство соотношений (23) – (25) основано на использовании леммы Гронуолла, согласно которой для функции 
, удовлетворяющей неравенству 
, где 
, 
, 
верна оценка
.
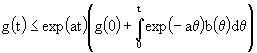Домножим скалярно уравнение (11) на 
. Получим:
. (26)
Принимая во внимание (17) и неравенство 
из (26) получаем
.
Из этого неравенства на основе леммы Гронуолла следует оценка (23).
Используя теперь (19), имеем 
. Это позволяет из (26) получить неравенство 
, из которого на основании леммы Гронуолла немедленно следует оценка (24).
Осталось теперь получит оценку (25). Для этого домножим скалярно уравнение (11) на 
, что дает
.
Для правой части имеем: 
. С учетом (19) приходим к неравенству
(27)
Принимая во внимание соотношения 
из (27) и лемму Гронуолла получим искомую оценку (25).
Смысл полученных оценок (23) - (25) состоит в том, что они устанавливают непрерывную зависимость решения нестационарной задачи (11) по начальным данным и правой части. Для рассматриваемых оценок существенно то, что для нормы решения задачи с однородной правой частью допускается экспоненциальный рост с инкрементом нарастания, который зависит от постоянных 
и 
.
Дополнительная информация:
© 2001-2024 Кафедра биофизики МГУ