. Пусть 
- множество внутренних узлов сетки:Без потери общности будем считать, что расчетная область представляет собой прямоугольник. В этой области введем равномерную (для простоты) по обеим переменным разностную сетку с шагами . Пусть - множество внутренних узлов сетки:
,
а 
- множество граничных узлов. Разностное решение задачи конвекции - диффузии на момент времени t обозначим 
. Введем обозначения для записи правой и левой разностных производных: 
, 
. Центральная разностная производная определяется выражением 
. Для сеточных функций, обращающихся в ноль на 
, определим гильбертово пространство Н, скалярное произведение и норму: 
, 
.
Разностный оператор диффузионного переноса 
на множестве функций 
определим выражением
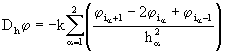. (36)
Разностный оператор 
самосопряжен в Н и имеет место оценка типа 
:
, (37)
где k – коэффициент диффузии,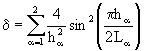 
, E – тождественный оператор. Полезна также и оценка сверху для разностного оператора 
(Самарский, 1983; Самарский, Николаев, 1978): 
, 
.
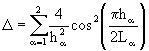Конвективные слагаемые в уравнении конвекции - диффузии аппроксимируем со вторым порядком на основе использования центральных разностных производных. Так, если используется запись оператора конвективного переноса в недивергентной форме, то
. (38)
Для уравнения конвекции - диффузии с конвективными слагаемыми в дивергентной форме разностный оператор конвективного переноса записывается в следующем виде:
. (39)
Для оператора конвективного переноса в симметричной форме имеем: 
, то есть
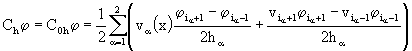. (40)
Отметим теперь основные свойства введенных разностных операторов конвективного переноса в Н. Для нахождения оператора, сопряженного 
, рассмотрим выражение
.
На множестве сеточных функций, обращающихся в ноль на 
, имеем
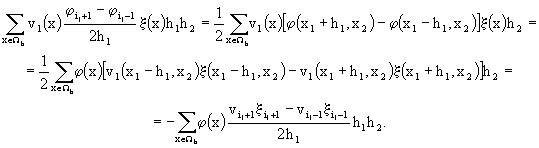
В силу этого 
. Таким образом, как и в непрерывном случае, для (38), (39)
, (41)
. (42)
Непосредственными выкладками можно убедиться в том, что на разностном уровне нет аналога оценки 
для рассматриваемых разностных операторов конвективного переноса. Поэтому использование симметричных аппроксимаций (40) конвективного переноса является более предпочтительным. Приходится ограничиваться более грубыми, по сравнению с исходной дифференциальной задачей, оценками сверху оператора конвективного переноса в дивергентной и недивергентной форме. Принимая во внимание неравенство
,
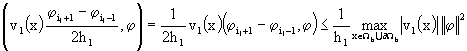получаем
, (43)
где теперь 
. Тем самым мы приходим к разностному аналогу неравенства 
, где постоянная величина 
определяется, в соответствии с (43), следующим образом: 
(напомним, что в случае дифференциального оператора конвективного переноса 
).
Получим теперь разностный аналог неравенства подчиненности оператора конвективного переноса оператору диффузионного переноса: 
. Для недивергентного разностного оператора конвективного переноса имеем
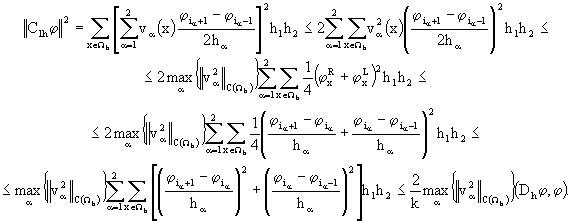
Поэтому при 
в неравенстве подчиненности 
можем положить 
. При 
аналогичную оценку получим на основе равенства
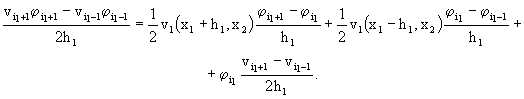
Как и в непрерывном случае, имеем
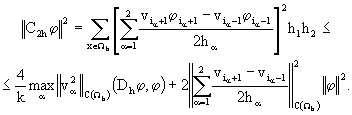
Воспользуемся разностным аналогом неравенства Фридрихса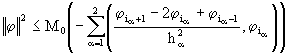 
. Здесь постоянная величина 
не зависит от шагов сетки. С помощью неравенства Фридрихса нетрудно получить искомое неравенство 
для разностного оператора конвективного переноса 
, в котором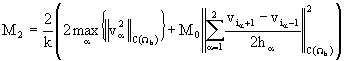 
. Аналогично, для случая 
имеем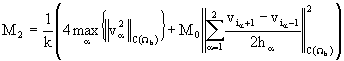 
.
Таким образом, для разностных операторов конвективного переноса имеют место оценки подчиненности 
с постоянными 
, полностью согласованными с непрерывным случаем при условии, что для аппроксимации дивергенции используются центральные разностные производные. При аппроксимации конвективных слагаемых в дивергентном и недивергентном видах постоянная 
зависит от шага сетки. Таким образом, варианты возможной аппроксимации конвективных слагаемых в дивергентной и недивергентной формах требуют дополнительного рассмотрения. Естественно пытаться строить такие аппроксимации, для которых постоянная 
в разностном операторе конвективного переноса была бы согласована с оператором конвективного переноса в непрерывном случае. В частности, если использовать операторы конвективного переноса в форме 
или 
, то по-прежнему сохраняется свойство кососимметричности оператора 
при любых v. Принимая во внимание эти соотношения, определим конвективные операторы в недивергентной и дивергентной формах следующими соотношениями:
, 
. (44)
В соответствии с (44) положим
, (45)
. (46)
При аппроксимациях (45), (46) имеет место неравенство 
, где постоянная величина 
определяется следующим образом: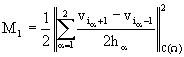 
, которая не зависит уже от параметров расчетной сетки и полностью согласована с постоянной 
для непрерывного случая.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ