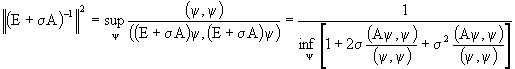Рассмотрим положительно полуопределенную матрицу 
, действующую на векторы из евклидова пространства. Имеет место следующее соотношение: 
для любых значений параметра 
. Действительно, по определению нормы оператора 
. Положим 
, тогда 
и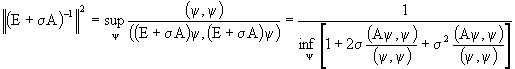 
. Поскольку оператор 
положительно полуопределенный, то из последнего равенства непосредственно следует и искомая оценка 
.
Сформулируем теперь Лемму Келлога, на которую будем неоднократно ссылаться в дальнейшем.
Лемма Келлога (Марчук, 1980; Марчук, 1988). Если 
и 
, то справедливо неравенство 
.
Доказательство. Введем обозначение 
и рассмотрим выражение для нормы этого оператора 
. Имеем: 
. (Здесь использовано введенное ранее соотношение 
). Преобразовывая последнее соотношение, окончательно получим: 
. Причем при доказательстве важное значение имеет условие положительной полуопределенности оператора (матрицы) А.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ