, 
, Введем на временном интервале 
аппроксимации операторов 
, 
так, чтобы 
. Схема многокомпонентного расщепления, построенная на основе элементарных схем Кранка - Николсона, представляет собой систему уравнений
. (24)
В случае, когда операторы 
коммутативны и 
или 
, данная схема является абсолютно устойчивой и имеет второй порядок аппроксимации по 
. Для некоммутативных операторов 
схема (24), вообще говоря, будет схемой первого порядка точности по 
. Докажем эти утверждения. Заметим, что система уравнений (24) сводится к одному уравнению
. (25)
Полагая 
, разложим по степеням малого параметра 
выражение 
. Поскольку 
, то сначала разложим в ряд операторы 
:
(26)
В результате получим
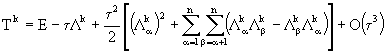. (27)
В случае, когда операторы 
коммутативны, выражение, стоящее под знаком двойной суммы, обращается в нуль и мы имеем
. (28)
Видно, что в этом случае схема имеет второй порядок аппроксимации по 
. Если же операторы 
некоммутативны, то схема расщепления имеет только первый порядок аппроксимации по 
. С помощью (25) найдем оценку вида
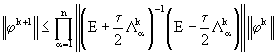. (29)
Из (29) на основании леммы Келлога следует, что
. (30)
Равенство будет иметь место в случае кососимметричных операторов 
. Таким образом, абсолютная устойчивость схемы (24) доказана. Реализация схемы (24) осуществляется путем последовательного решения системы уравнений, аналогичных уравнениям (23).
Общий подход к покомпонентному расщеплению на основе элементарных схем Кранка - Николсона состоит в том, что во многих случаях целесообразно применить предварительное расщепление исходной эволюционной задачи на систему дифференциальных уравнений с надлежащим образом выбранными в ней операторами 
. Каждое уравнение системы затем аппроксимируется схемой Кранка - Николсона с возможным дополнительным расщеплением 
на 
, так что 
, где 
.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ