Метод двуциклического покомпонентного расщепления. Случай оператора

Рассмотрим теперь еще один класс методов расщепления - методы двуциклического покомпонентного расщепления (Марчук, 1982; Марчук, 1988). В них отсутствует требование коммутативности операторов в представлении . Начнем с рассмотрения однородной задачи (1.1) - (1.2), в которой оператор А зависит от времени и его можно представить в виде суммы положительно полуопределенных матриц: , , , имеющих достаточно гладкие по t элементы. Рассмотрим аппроксимации этих матриц не на интервале , как в (17), а на интервале . Положим и запишем две системы разностных уравнений

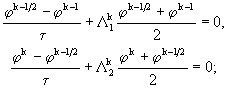(31.1)

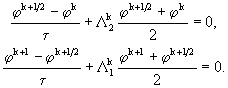(31.2)

Цикл вычислений состоит в поочередном применении схем (31.1), (31.2). Из данных схем, последовательно исключая , , , получаем, что на полном шаге вычислений имеет место операторное уравнение

, (32)

где оператор шага имеет следующий вид:

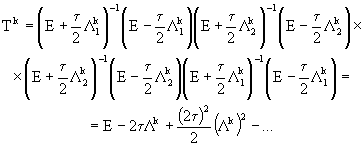(33)

Здесь и далее предполагается выполнение ограничения (20): . Если , то при достаточной гладкости решения задачи и элементов матриц система разностных уравнений (31.1) - (31.2) абсолютно устойчива и схема (32) аппроксимирует исходную задачу со вторым порядком точности по . В самом деле, из разложения оператора шага заключаем, что он с точностью до величины совпадает с оператором шага схемы Кранка - Николсона, примененной к удвоенному интервалу по времени. Следовательно, независимо от коммутативности операторов , схема имеет второй порядок аппроксимации по . Таким образом, этот прием снимает весьма сильное требование коммутативности операторов. Устойчивость схемы следует из оценок в норме :

, (34)

поскольку в силу леммы Келлога .

Рассмотрим теперь неоднородную задачу (3.1) - (3.2). Для нее схема двуциклического покомпонентного расщепления имеет следующий вид

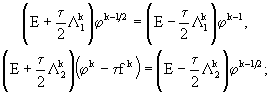(35.1)

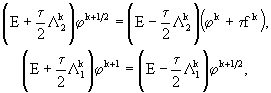(35.2)

где . Разрешая эти уравнения относительно , получаем

, (36)

где , . С помощью разложения по степеням малого параметра придем к соотношению

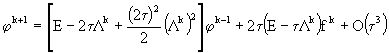, (37)

которое, в свою очередь, преобразуем к виду

. (38)

Исключим , используя разложение решения в ряд Тейлора в окрестности точки . С точностью до имеем

. (39)

Производную исключим с помощью соотношения

. (40)

Из (39), (40) получаем:

. (41)

Отсюда

. (42)

Подставим соотношение (42) в (38):

. (43)

Если теперь принять, что , , то легко заметить, что уравнение (43) аппроксимирует исходную задачу в норме на интервале со вторым порядком по . Устойчивость схемы доказывается просто. Оценим (36) по норме