, 
, Пусть теперь 
и все операторы 
положительно полуопределенные: 
. Рассмотрим случай однородных уравнений (1.1) - (1.2). Исходная система сначала решается на интервале 
для 
, а затем на интервале 
, но уже в обратном порядке для 
:
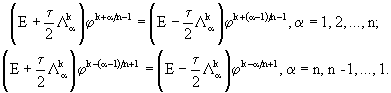(47)
Очевидно, что для полного цикла (47) имеем соотношение, аналогичное по форме (32) (то есть 
), но с оператором шага в виде 
. Таким образом, на интервале 
схема (47) имеет второй порядок точности по 
, если в качестве 
взят один из операторов вида 
, 
.
Для неоднородной задачи (3.1) - (3.2) на интервале 
схема двуциклического многокомпонентного расщепления имеет вид
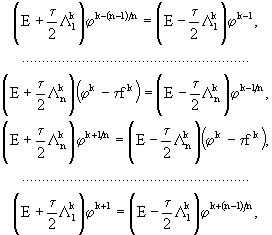(48)
где 
. Эта схема, как и для случая n = 2, в предположении необходимой гладкости имеет второй порядок аппроксимации по 
и абсолютно устойчива.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ