В конечномерном гильбертовом пространстве Н рассмотрим матричную однородную эволюционную задачу (1.1) - (1.2)
![]() в
в ![]() ,
,
![]() при t = 0,
при t = 0,
где ![]() . Для простоты ограничимся случаем положительного оператора А, не зависящего от времени. Тем самым при таком расщеплении мы предполагаем, что оба оператора являются неотрицательными. Ставится задача построения приближенного решения задачи (1.1) - (1.2) с использованием такой схемы, которая по своим вычислительным затратам эквивалента решению задачи Коши для уравнений
. Для простоты ограничимся случаем положительного оператора А, не зависящего от времени. Тем самым при таком расщеплении мы предполагаем, что оба оператора являются неотрицательными. Ставится задача построения приближенного решения задачи (1.1) - (1.2) с использованием такой схемы, которая по своим вычислительным затратам эквивалента решению задачи Коши для уравнений ![]() ,
, ![]() , то есть решению более простых (в некотором смысле) задач. Схема переменных направлений для этой задачи имеет вид
, то есть решению более простых (в некотором смысле) задач. Схема переменных направлений для этой задачи имеет вид
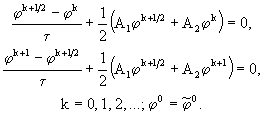 (60)
(60)
В такой форме она была предложена Писменом, Рэкфордом и Дугласом (Douglas, 1956; Douglas, 1958; Douglas, Gunn, 1963; Douglas, Gunn, 1964; Peaceman, Rachford, 1955) в применении к параболической задаче с двумя пространственными переменными. При этом оператор ![]() являлся разностной аппроксимацией одномерного дифференциального оператора
являлся разностной аппроксимацией одномерного дифференциального оператора ![]() . Отметим, что схема (60) в этом случае симметрична, то есть в ней
. Отметим, что схема (60) в этом случае симметрична, то есть в ней ![]() и
и ![]() меняются ролями от первого дробного шага ко второму (чем и обусловлено название метода). Решение каждого из этих уравнений в параболической задаче легко реализуется методом прогонки, поэтому схему (60) называют также схемой продольно-поперечной прогонки. Если в (60) исключить промежуточное решение
меняются ролями от первого дробного шага ко второму (чем и обусловлено название метода). Решение каждого из этих уравнений в параболической задаче легко реализуется методом прогонки, поэтому схему (60) называют также схемой продольно-поперечной прогонки. Если в (60) исключить промежуточное решение ![]() , то получим
, то получим
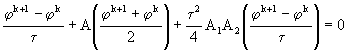 . (61)
. (61)
Сравнивая выражение (61) со схемой Кранка - Николсона (8), заключаем, что она обладает вторым порядком аппроксимации по ![]() . Далее, если рассматривать (60), когда
. Далее, если рассматривать (60), когда ![]() есть трехточечная аппроксимация оператора
есть трехточечная аппроксимация оператора ![]() :
: ![]() , то легко установить, что данная схема абсолютно устойчива.
, то легко установить, что данная схема абсолютно устойчива.
В случае неоднородной системы уравнений (3.1) - (3.2)
![]() в
в ![]() ,
,![]() ,
,
![]() при t = 0
при t = 0
необходимо решить задачи Коши для уравнений ![]() ,
, ![]() . При приближенном решении для правой части также используется аддитивное представление
. При приближенном решении для правой части также используется аддитивное представление ![]() . Разностная схема переменных направлений Писмена - Рекфорда (Peaceman, Rachford, 1955) для задачи (3.1) - (3.2) при сделанных выше предположениях состоит из двух шагов. Сначала по известному значению
. Разностная схема переменных направлений Писмена - Рекфорда (Peaceman, Rachford, 1955) для задачи (3.1) - (3.2) при сделанных выше предположениях состоит из двух шагов. Сначала по известному значению ![]() находится вспомогательная сеточная функция, которую мы обозначим
находится вспомогательная сеточная функция, которую мы обозначим ![]() , из уравнения
, из уравнения
![]() . (62.1)
. (62.1)
Интерпретируя ![]() как решение на момент времени
как решение на момент времени ![]() , можно отметить, что уравнение (62.1) соответствует решению по чисто неявной схеме для оператора
, можно отметить, что уравнение (62.1) соответствует решению по чисто неявной схеме для оператора ![]() и по явной схеме для оператора
и по явной схеме для оператора ![]() . В силу этого второй шаг метода переменных направлений будет соответствовать использованию уравнения
. В силу этого второй шаг метода переменных направлений будет соответствовать использованию уравнения
![]() . (62.2)
. (62.2)
Уравнение (62.2), наоборот, соответствует решению по чисто неявной схеме для оператора ![]() и по явной схеме для оператора
и по явной схеме для оператора ![]() . При расщеплении по пространственным переменным, например, при решении краевой задачи для двухмерного параболического уравнения первый шаг связывается с использованием чисто неявной схемы по первой переменной и явной - по второй переменной. Второй шаг основан на применении явной схемы по первой переменной и неявной - по второй переменной. При такой интерпретации схема (62.1), (62.2) называется схемой переменных направлений. Реализация схемы переменных направлений (62.1), (62.2) основана на определении
. При расщеплении по пространственным переменным, например, при решении краевой задачи для двухмерного параболического уравнения первый шаг связывается с использованием чисто неявной схемы по первой переменной и явной - по второй переменной. Второй шаг основан на применении явной схемы по первой переменной и неявной - по второй переменной. При такой интерпретации схема (62.1), (62.2) называется схемой переменных направлений. Реализация схемы переменных направлений (62.1), (62.2) основана на определении ![]() и
и ![]() из уравнений
из уравнений
![]() , (63.1)
, (63.1)
![]() . (63.2)
. (63.2)
Запись (63.1), (63.2) указывает на то, что при расщеплении по пространственным переменным решение находится обращением соответствующего одномерного сеточного оператора методом прогонки сначала по одной переменной (одному направлению), потом - по другой (другому направлению).
Приведем априорную оценку, выражающую устойчивость схемы переменных направлений (62.1) - (62.2) по начальным данным и правой части. Пусть в схеме (62.1) - (62.2) постоянные операторы ![]() . Тогда для разностного решения имеет место следующая оценка устойчивости по начальным данным и правой части:
. Тогда для разностного решения имеет место следующая оценка устойчивости по начальным данным и правой части:
![]() . (64)
. (64)
Исследование устойчивости основано на операторном неравенстве
![]() . (65)
. (65)
Имеем ![]() , поэтому неравенство (65) справедливо для операторов
, поэтому неравенство (65) справедливо для операторов ![]() и в том случае, если
и в том случае, если ![]() , то есть при
, то есть при ![]() . Из (63.1), (63.2) непосредственно следует
. Из (63.1), (63.2) непосредственно следует
![]() , (66.1)
, (66.1)
![]() . (66.2)
. (66.2)
На основании (65), полагая ![]() , из (66.1), (66.2) получим
, из (66.1), (66.2) получим
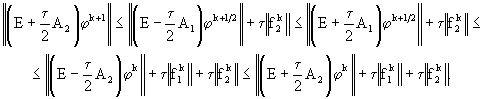
С помощью рекуррентного неравенства ![]() , исключая промежуточные значения решения, получаем искомую априорную оценку (64), из которой заключаем об устойчивости схемы по начальным данным и правой части.
, исключая промежуточные значения решения, получаем искомую априорную оценку (64), из которой заключаем об устойчивости схемы по начальным данным и правой части.
Если проанализировать с помощью метода Неймана поведение ошибки по каждому направлению ![]() , то оказывается, что на первом полушаге ошибка в направлении
, то оказывается, что на первом полушаге ошибка в направлении ![]() уменьшается, а в направлении
уменьшается, а в направлении ![]() увеличивается, затем, на втором полушаге, ошибка в направлении
увеличивается, затем, на втором полушаге, ошибка в направлении ![]() возрастает, а в направлении
возрастает, а в направлении ![]() убывает. Однако, как бы сильно ни выросла ошибка в каком-либо направлении на данном полушаге, на следующем она непременно уменьшится, так что в целом на двух полушагах она не возрастает по модулю (Яненко, 1967). В этой же работе отмечается, что схема метода переменных направлений оказывается непригодной для трехмерной параболической задачи, поскольку в этом случае схема не является абсолютно устойчивой. Поэтому во многих задачах предпочтительны схемы метода стабилизирующей поправки (которые вместе со схемой переменных направлений иногда называют также неявными схемами переменных направлений).
убывает. Однако, как бы сильно ни выросла ошибка в каком-либо направлении на данном полушаге, на следующем она непременно уменьшится, так что в целом на двух полушагах она не возрастает по модулю (Яненко, 1967). В этой же работе отмечается, что схема метода переменных направлений оказывается непригодной для трехмерной параболической задачи, поскольку в этом случае схема не является абсолютно устойчивой. Поэтому во многих задачах предпочтительны схемы метода стабилизирующей поправки (которые вместе со схемой переменных направлений иногда называют также неявными схемами переменных направлений).
СхемыстабилизирующейпоправкибылипредложеныДугласомиРэкфордом (Douglas, Rachford, 1956) для решения трехмерного уравнения теплопроводности. Так, если ![]() , то эта схема для однородного уравнения имеет следующий вид:
, то эта схема для однородного уравнения имеет следующий вид:
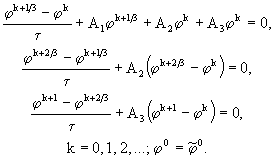 (67)
(67)
Исключая из (67) промежуточные значения ![]() и
и ![]() , придем к уравнению
, придем к уравнению
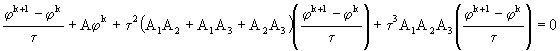 . (68)
. (68)
Отсюда следует, что схема имеет первый порядок точности по ![]() . Рассматривая ее для уравнения теплопроводности, легко установить, что она абсолютно устойчива. Кроме того, здесь структура схемы такова: первый дробный шаг дает полную аппроксимацию уравнения теплопроводности, следующие дробные шаги являются поправочными и используются для улучшения устойчивости. Поэтому такие схемы и называют схемамистабилизирующей поправки, или схемами с поправкой на устойчивость.
. Рассматривая ее для уравнения теплопроводности, легко установить, что она абсолютно устойчива. Кроме того, здесь структура схемы такова: первый дробный шаг дает полную аппроксимацию уравнения теплопроводности, следующие дробные шаги являются поправочными и используются для улучшения устойчивости. Поэтому такие схемы и называют схемамистабилизирующей поправки, или схемами с поправкой на устойчивость.
Абсолютно устойчивая схема второго порядка аппроксимации предложена Дугласом (Douglas, 1958) и имеет следующий вид:
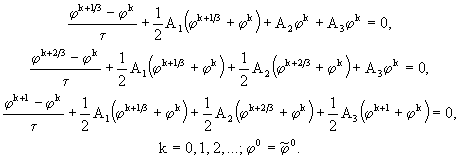 (69)
(69)
Эту схему можно переписать также в виде
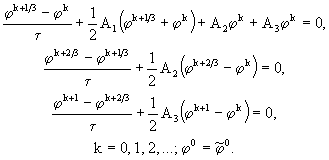 (70)
(70)
Если исключить из (70) промежуточные значения ![]() и
и ![]() , придем к уравнению
, придем к уравнению
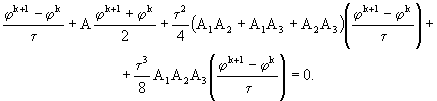 (71)
(71)
Отсюда и заключаем, что схема (69) действительно имеет второй порядок аппроксимации по времени (Марчук, 1988).
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ