в 
,
,В конечномерном гильбертовом пространстве Н рассмотрим неоднородную задачу (3.1) - (3.2)
в ,,
при t = 0.
при двухкомпонентном расщеплении на два постоянных неотрицательных оператора 
, 
. Для приближенного решения исходной задачи построим двухслойную разностную схему, которая имеет канонический вид (Самарский, Вабищевич, 1999)
. (72)
Факторизованная схема соответствует выбору оператора 
в виде 
, где 
. При таком задании 
каждый из операторов 
соответствует использованию обычной схемы с весами для отдельного операторного слагаемого. Вычислительная реализация факторизованной схемы связана с решением двух задач:
(73)
При расщеплении по пространственным переменным в двухмерной параболической задаче последовательно решаются одномерные задачи, связанные с дифференциальным оператором по соответствующему направлению. В некоторых случаях и схемы переменных направлений записываются в виде факторизованных схем.
Прямое исследование устойчивости факторизованных схем на основе проверки необходимых и достаточных условий затруднено в силу несамосопряженности операторов, неположительности оператора 
. Поэтому обычно пытаются доказывать устойчивость схемы в более сложных нормах. Пусть в факторизованной схеме 
- постоянные операторы. Тогда при 
схема безусловно устойчивая и для решения имеет место априорная оценка
. (74)
Запишем каноническую схему (72) в следующем виде: 
. Отсюда получим
. (75)
Добавим и вычтем из правой части (75) слагаемое, равное 
, что дает
. (76)
Принимая во внимание 
, получим
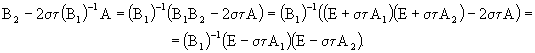(77)
Обозначим 
и перепишем (76) в виде
. (78)
С учетом (77) для оператора Q получим представление
.
В силу этого запишем Q в виде
(79)
где
(80)
В силу леммы Келлога из (80) получим, что 
. С учетом (79) не превосходит единицы и норма оператора Q, поэтому из (78) следует неравенство 
при всех 
. Тем самым приходим к доказываемой оценке (74) для разностного решения.
На основе полученной оценки устойчивости показано, что при 
факторизованная схема сходится со вторым порядком точности по 
, а при 
- с первым.
Для построения безусловно устойчивых факторизованных схем в настоящее время широко используется принцип регуляризации разностных схем (Самарский, 1967).
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ