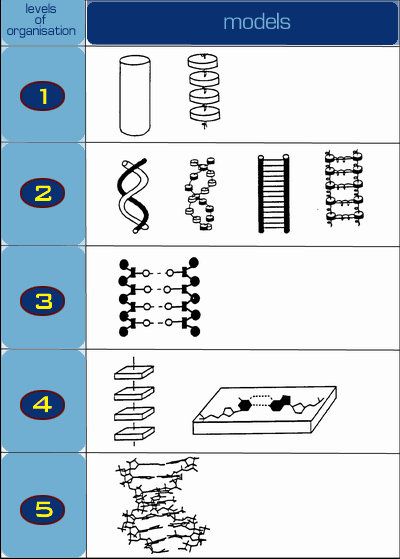
Рис. 17. Уровни моделирования
подвижности ДНК При моделировании функциональных движений ДНК плодотворным оказался поиск подходящего механического аналога, то есть хорошо изученной в механике модельной системы с аналогичным набором структурных элементов, движений и взаимодействий. Существуют сотни различных моделей, описывающих движения ДНК: континуальные и дискретные, спиральные, и игнорирующие спиральную структуру, имитирующие движение каждого или почти каждого атома фрагмента, и имитирующие движения только основных субъединиц, однородные модели, и модели, учитывающие наличие последовательности оснований.
Самые простые - модели эластичного стержня с круговым сечением (уровень 1 на рисунке). Дискретным аналогом является цепочка
связанных друг с другом дисков (или бусинок), причем каждому диску соответствует
одна или несколько нуклеотидных пар. Динамика эластичного стержня
характеризуется тремя типами внутренних движений: продольными смещениями,
вращательными, или торсионными движениями и поперечными смещениями. Решением
системы уравнений являются обычные плоские волны, а спектр колебаний ДНК состоит
только из трех акустических ветвей: продольной, поперечной и изгибной.
Модели второго уровня учитывают, что молекула ДНК
состоит из двух полинуклеотидных цепочек, ее можно смоделировать при помощи двух
эластичных стержней, слабо взаимодействующих между собой и свернутых в двойную
спираль. Дискретный аналог такой модели представляет собой две цепочки дисков,
связанных друг с другом продольными и поперечными пружинами, причем жесткость
продольных пружин много больше, чем жесткость поперечных. Спектр торсионных
колебаний, рассчитанных по такой (линейной) модели состоит из двух ветвей:
акустической и оптической.
Третий уровень иерархии учитывает тот факт, что
каждая из цепочек состоит из трех субъединиц: сахаров, фосфатов и оснований.
Четвертый уровень представляют решеточные модели ДНК,
описывающие движения атомов, составляющих решеточную ячейку. (Powell et al., Phys.Rev. A-35, 1987). Задачи такого рода
удается решить в линейном (гармоническом) приближении и получить сложные спектры
ДНК, содержащие множество ветвей. Модели пятого уровня
максимально точно передают структуру и движения ДНК (модели молекулярной
динамики).
 |
Рис. 17. Уровни моделирования
подвижности ДНК |
Пионерской работой в области изучения внутренней динамики ДНК явилось
исследование Инглендера с соавторами. (Englander, Kallenbach,
Heeger, Krumhansl, Litwin, 1980). Методом водородно-тритиевого обмена
была показана принципиальная возможность образования в ДНК открытых состояний,
определяемых как мобильные локальные области (длиной от одной до нескольких пар
оснований), внутри которых водородные связи разорваны. Образование таких
открытых состояний связано со значительными угловыми отклонениями оснований от
положений равновесия. Математически этот процесс был описан с помощью
гамильтонова формализма, широко применяемого в теоретической и математической
физике. При моделировании внутренней подвижности ДНК авторы не ограничились
моделированием малых отклонений от положения равновесия (гармоническое или
линейное приближение), а рассмотрели движения большой амплитуды (ангармоническое
или нелинейное приближение). Было показано, что нелинейные волновые решения
синус-уравнения Гордона
являются теми математическими образами, которые могут имитировать открытые
состояния ДНК. Здесь функция j (z,t)
Модификации модели Инглендера (Yakushevich, 1998)
описывает процессы вращательных движений оснований вокруг сахаро-фосфатных
цепочек, характеризующиеся большой амплитудой. Эти движения приводят к разрыву
водородных связей и образованию открытых состояний. При описании динамических
свойств используется аналогия между молекулой ДНК и цепочкой связанных
маятников. Роль вращающихся маятников в молекуле ДНК играют основания,
присоединенные к сахарам, роль горизонтальной цепочки - сахаро-фосфатная
цепочка, роль внешнего гравитационного поля - поле, наводимое второй нитью ДНК,
слабо взаимодействующей с первой через водородные связи между основаниями.
Динамика цепочки маятников хорошо изучена и описывается набором n нелинейных уравнений. Для n-го
маятника уравнение имеет вид:
где jnn-го маятника от положения равновесия, I - момент инерции маятника, K -
коэффициент жесткости горизонтальной цепочки, m и h - масса маятника и его длина, соответственно, g - гравитационная постоянная. Если перейти к континуальному
приближению, можно записать уравнение для динамики вращательных колебаний
оснований ДНК
где I0 - момент инерции основания, К0 - коэффициент жесткости сахаро-фосфатной цепочки,
V0 sin - сила, действующая между
основаниями внутри пар.
j
Это уравнение типа синус-Гордона имеет решение вида "кинк",
Здесь g = [1-
Iv2 / K0 a2]-1/2; x = z - vt; vd =
(K0a2 / V0)1/2; a -
расстояние между ближайшими вдоль цепи парами оснований. Качественная картина,
соответствующая этому решению, приведена на рис.18
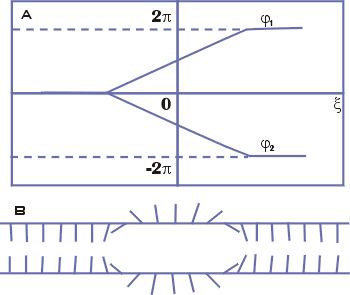 |
Рис. 18. Схема расплетания
ДНК. |
Две сахаро-фосфатные цепочки ДНК изображены двумя длинными линиями, а
основания - множеством коротких линий. Кинку соответствует локальная область с
разорванными парами оснований. Решение (34)
описывает локальную деформацию (раскрытие пар оснований), движущуюся вдоль
молекулы ДНК со скоростью v. В процессе распространения
волны может наблюдаться ускорение вследствие постоянной подкачки энергии и
замедление вследствие эффектов внутреннего трения. Учет неоднородностей ДНК в
виде блоков с преимущественным содержанием G-C пар на
фоне остальной части молекулы, в основном содержащей A-T
пары, позволяет оценить минимальное значение скорости нелинейной волны,
необходимое для преодоления барьера из G-C блоков и
преодоления движения. Рассмотренная модель позволяет качественно объяснить
эффекты дальнодействия в молекуле ДНК и распространение конформационных волн
через регуляторные области, что имеет особенно важное значение для регуляции
функциональной активности ДНК. Нелинейные конформационные волны, движущиеся
вдоль ДНК, могут также играть роль в координации работы нескольких генов.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ